题目内容
如图所示，ad、bd、cd是竖直面内三根固定的光滑细杆，a、b、c、d位于同一圆周上，a点为圆周的最高点，d点为最低点．每根杆上都套着一个完全相同的小滑环（图中未画出），三个滑环分别从a、b、c点无初速释放，关于它们下滑过程的下列说法中正确的是（ ）分析：根据牛顿定律与运动学公式结合分析得到：三个滑环下滑的时间相同．由冲量公式I=Ft，判断重力冲量关系．由于c环受到的弹力最大，其冲量最大．a环加速度最大，合力最大，其冲量最大．下滑过程中，只有重力做功，根据动能定理得知，动能的增量等于重力做功，重力对a环做功最大，其动能的增量最大．
解答：解：设任一细杆与竖直方向的夹角为α，环运动的时间为t，圆周的直径为D．则环的加速度大小a=gcosα．
由位移公式得：Dcosα=
at2=
gcosαt2，得到t=
，所以三个环运动时间相同．
A、由于三个环的重力相等，运动时间相同，由公式I=Ft分析可知，各环重力的冲量相等．故A错误．
B、c环受到的弹力最大，运动时间相等，则弹力对环c的冲量最大．故B正确．
C、a环的加速度最大，受到的合力最大，则合力对a环的冲量最大．故C错误．
D、重力对a环做功最大，其动能的增量最大．故D错误．
故选B
由位移公式得：Dcosα=
| 1 |
| 2 |
| 1 |
| 2 |
|
A、由于三个环的重力相等，运动时间相同，由公式I=Ft分析可知，各环重力的冲量相等．故A错误．
B、c环受到的弹力最大，运动时间相等，则弹力对环c的冲量最大．故B正确．
C、a环的加速度最大，受到的合力最大，则合力对a环的冲量最大．故C错误．
D、重力对a环做功最大，其动能的增量最大．故D错误．
故选B
点评：本题关键之处是运用牛顿定律和运动学公式分析三个环的运动时间关系，中等难度．
练习册系列答案
相关题目
（2004?江西）如图所示，ad、bd、cd是竖直面内三根固定的光滑细杆，a、b、c、d位于同一圆周上，a点为圆周的最高点，d点为最低点．每根杆上都套着一个小滑环（图中未画出），三个滑环分别从a、b、c处释放（初速为0），用t1、t2、t3依次表示滑环到达d所用的时间，则（ ）
（2011?甘肃二模）如图所示，AD、BD、CD都是光滑的直角斜面，斜面固定在水平地面上，现使一小物体分别从A、B、C点由静止开始下滑到D点，所用时间分别为t1、t2、t3，则（ ）
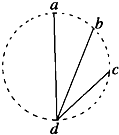如图所示，ad、bd、cd是竖直面内三根固定的光滑细杆，a、b、c、d位于同一圆周，a点为圆周的最高点，d为圆周的最低点．每根杆上都套着一个质量相同的小滑环（图中未画出），三个滑环分别a、b、c处释放（初速度为零），关于它们下滑的过程，下列说法中正确的是（ ）| A、重力对它们的冲量相同 | B、弹力对它们的冲量相同 | C、合外力对它们的冲量相同 | D、它们的动能增量相同 |
如图所示，ad、bd、 cd是竖直面内的三根固定的光滑细杆，a、ｂ、c、ｄ位于同一圆周上，ａ点为圆周上最高点，ｄ点为圆周上最低点。每根杆上都套有一个小圆环，三个圆环分别从ａ、ｂ、c处由静止释放，用t1 、t2、t3依次表示各环到达d点所用的时间，则（ ）
| A．t 1＜t2＜ t3 | B．t 1＞t2＞ t3 |
| C．t 3＞t1＞ t2 | D．t 1＝t2＝t3 |