题目内容
如图所示，左图是杭州儿童乐园中的过山车的实物图片，右图是过山车的原理图．在原理图中，半径分别为R1＝2.0 m和R2＝8.0 m的两个光滑圆形轨道固定在倾角为α＝37°斜轨道面上的Q、Z两点，且两圆形轨道的最高点A、B均与P点平齐，圆形轨道与斜轨道之间圆滑连接．现使质量m＝20 kg的小车(视作质点)从P点以一定的初速度沿斜轨道向下运动．已知斜轨道面与小车间的动摩擦因数为μ＝
，g＝10 m/s2，sin37°＝0.6，cos37°＝0.8．问：
(1)若小车能通过A、B两点，则小车在P点的初速度满足什么条件？
(2)若小车恰好能通过第二个圆形轨道的最高点B，则小车通过第一个圆形轨道最低点时，对轨道的压力大小是多少？
答案：
解析：
解析：
|
(1)解：在B有： P点到B点的过程，由动能定理得： 其中， 解得： (2)通过(1)问中的解可知，小车恰好能通过第二个圆形轨道的最高点B时，小车在P点初速度为 P点到A点的过程，由动能定理得： 设小车通过第一个圆形轨道最低点时的速度 由牛顿定律得： 根据牛顿第三定律可得压力为1920 N． |
为PZ之间的距离，根据几何关系可知满足：
即小车在P点初速度满足的条件为
．
为PQ之间的距离，根据几何关系可知满足：
，由机械能守恒定律得：
，
解得：
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
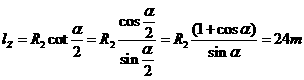
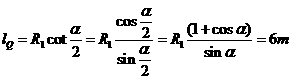
=37°斜轨道面上的Q、Z两点,且两圆形轨道的最高点A、B均与P点平齐,圆形轨道与斜轨道之间圆滑连接.现使质量
的小车(视作质点)从P点以一定的初速度沿斜轨道向下运动.已知斜轨道面与小车间的动摩擦因数为
=
,g=10 m/s2,sin 37°=0.6,cos 37°=0.8.问:
=37°斜轨道面上的Q、Z两点,且两圆形轨道的最高点A、B均与P点平齐,圆形轨道与斜轨道之间圆滑连接.现使质量
的小车(视作质点)从P点以一定的初速度沿斜轨道向下运动.已知斜轨道面与小车间的动摩擦因数为
=
,g="10" m/s2,sin 37°="0.6,cos" 37°=0.8.问:
=37°斜轨道面上的Q、Z两点,且两圆形轨道的最高点A、B均与P点平齐,圆形轨道与斜轨道之间圆滑连接.现使质量
的小车(视作质点)从P点以一定的初速度沿斜轨道向下运动.已知斜轨道面与小车间的动摩擦因数为
=
,g=10 m/s2,sin 37°=0.6,cos 37°=0.8.问:
=37°斜轨道面上的Q、Z两点,且两圆形轨道的最高点A、B均与P点平齐,圆形轨道与斜轨道之间圆滑连接.现使质量
的小车(视作质点)从P点以一定的初速度沿斜轨道向下运动.已知斜轨道面与小车间的动摩擦因数为
=
,g=10 m/s2,sin 37°=0.6,cos 37°=0.8.问: