题目内容
13.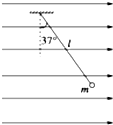 一根长为l的丝线吊着一质量为m,带电荷量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成37°角,先突然将该电场方向变为向下且大小不变,不考虑因电场的改变而带来的其它影响(重力加速度为g,sin37°=0.6,cos37°=0.8)求:
一根长为l的丝线吊着一质量为m,带电荷量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成37°角,先突然将该电场方向变为向下且大小不变,不考虑因电场的改变而带来的其它影响(重力加速度为g,sin37°=0.6,cos37°=0.8)求:(1)匀强电场的电场强度的大小
(2)求小球经过最低点时丝线的拉力大小.
分析 (1)以小球为研究对象,分析受力情况,由于小球处于静止状态,合力为零,由平衡条件分析电场力的方向,求解电场强度大小;
(2)当电场方向变为向下后,小球受到的电场力竖直向下,向下做圆周运动,根据动能定理求解小球经过最低点时的瞬时速度;小球经过最低点时,由重力、电场力和丝线的拉力的合力提供了向心力,根据牛顿第二定律求解丝线对小球的拉力.
解答 解:(1)小球静止在电场中受力如下图所示,显然小球带正电,由平衡条件得:

mgtan37°=qE…①
故有:E=$\frac{3mg}{4q}$…②
(2)电场方向变成向下后,小球开始摆动做圆周运动,重力、电场力对小球做正功.由动能定理得:
$\frac{1}{2}$mv2=(mg+qE)l(1-cos37°)…③
由圆周运动知识,在最低点时,小球受力情况如下图所示,由牛顿第二定律有:
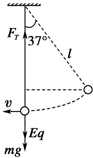
FT-(mg+qE)=m$\frac{{v}^{2}}{l}$…④
由③④解得:FT=$\frac{49}{20}$mg.
答:
(1)匀强电场的电场强度的大小为$\frac{3mg}{4q}$;
(2)小球经过最低点时丝线的拉力为$\frac{49}{20}$mg.
点评 运用动能定理求速度,根据牛顿第二定律求丝线的拉力,是常用的方法和思路,要能熟练运用力学方法解决电场中的问题.

练习册系列答案
相关题目
4.关于物体的运动状态和所受合外力的关系,下列说法正确的是( )
| A. | 物体所受的合外力为零时,物体一定处于静止状态 | |
| B. | 只有在合外力发生变化时,物体的运动状态才会改变 | |
| C. | 物体所受的合外力不为零时,物体就一定有加速度 | |
| D. | 物体的运动方向一定与它所受的合外力的方向相同 |
2.从发现情况到采取相应措施经过的时间叫人的反应时间.现甲同学用两根手指捏住木尺顶端,乙同学一只手在木尺下端靠近木尺但不接触木尺且准备握住木尺.当乙同学看到甲同学放手时,立即握住木尺,测出木尺下落高度为19.6cm,g=9.8m/s2,则( )
| A. | 甲同学反应时间为0.2s | B. | 甲同学反应时间为2s | ||
| C. | 乙同学反应时间为0.2s | D. | 乙同学反应时间为2s |
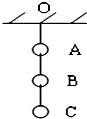 如图所示,在竖直向上的匀强电场中有三个小球A、B、C,用不可伸长的绝缘丝线相连悬挂于O点,质量分别为5m,3m和2m,其中只有B球带负电-q,电场强度为E.现将AO线烧断,在烧断瞬间,aA=$\frac{qE}{8m}+g$m/s2;aB=$\frac{qE}{8m}+g$m/s2; aC=gm/s2.
如图所示,在竖直向上的匀强电场中有三个小球A、B、C,用不可伸长的绝缘丝线相连悬挂于O点,质量分别为5m,3m和2m,其中只有B球带负电-q,电场强度为E.现将AO线烧断,在烧断瞬间,aA=$\frac{qE}{8m}+g$m/s2;aB=$\frac{qE}{8m}+g$m/s2; aC=gm/s2.



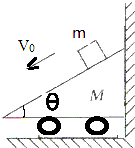 如图所示,质量为M的小车放在光滑的水平地面上,右面靠墙,上表面是一个光滑的斜面,斜面的倾角为θ,设当地的重力加速度为g,那么,当有一个质量为m的物块在这个斜面上以初速度为V0开始下滑后,求:
如图所示,质量为M的小车放在光滑的水平地面上,右面靠墙,上表面是一个光滑的斜面,斜面的倾角为θ,设当地的重力加速度为g,那么,当有一个质量为m的物块在这个斜面上以初速度为V0开始下滑后,求: