题目内容
11.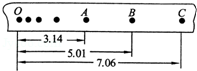 在《验证机械能守恒定律》的实验中,质量m=1kg的重物自由下落,在纸带上打出一系列的点,如图所示(相邻计数点时间间隔为0.02s),单位cm,那么
在《验证机械能守恒定律》的实验中,质量m=1kg的重物自由下落,在纸带上打出一系列的点,如图所示(相邻计数点时间间隔为0.02s),单位cm,那么 (1)打点计时器打下计数点B时,物体的速度是:0.98m/s.
(2)从起点O到打下计数点B的过程中重力势能减少量△Ep=0.491J,此过程中物体动能的增加量△Ek0.480J(g取9.8m/s2)
(3)通过计算,数值上△Ep=>△Ek(填“>”“=”或“<”),这是因为阻力的存在,一部分重力势能转化为内能.
(4)实验的结论是在误差允许的范围内,重物的机械能守恒..
分析 根据某段时间内的平均速度等于中间时刻的瞬时速度得出B点的速度,从而得出动能的增加量,结合下降的高度求出重力势能的减小量,从而验证机械能是否守恒.
解答 解:(1)B点的瞬时速度${v}_{B}=\frac{{x}_{AC}}{2T}=\frac{(7.06-3.14)×1{0}^{-2}}{0.04}m/s$=0.98m/s.
(2)从起点O到打下计数点B的过程中重力势能减少量△Ep=mgh=1×9.8×5.01×10-2J≈0.491J.
物体动能的增加量$△{E}_{k}=\frac{1}{2}m{{v}_{B}}^{2}=\frac{1}{2}×1×0.9{8}^{2}$J≈0.480J.
(3)通过计算,数值上△Ep>△Ek,这是因为阻力的存在,一部分重力势能转化为内能.
(4)实验的结论是:在误差允许的范围内,重物的机械能守恒.
故答案为:(1)0.98m/s,(2)0.491J,0.480J,(3)>,阻力的存在,一部分重力势能转化为内能(4)在误差允许的范围内,重物的机械能守恒.
点评 解决本题的关键知道验证机械能守恒的实验原理,掌握处理纸带的方法,通过平均速度求解瞬时速度,从而求解动能的变化量,通过下降高度求解重力势能的减小量.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
2.短跑运动员在100m比赛中,以8m/s的速度迅速从起点冲出,到50m处的速度是9m/s,10s末到达终点的速度是10.3m/s,则运动员在全程中的平均速度是( )
| A. | 10m/s | B. | 9.1m/s | C. | 9m/s | D. | 7.5m/s |
19. 如图所示,ABCD为固定的水平光滑矩形金属导轨,处在方向竖直向下,磁感应强度为B的匀强磁场中,A、B间距为L,左右两端均接有阻值为R的电阻,质量为m、长为L且不计电阻的导体棒MN放在导轨上,与导轨接触良好,与左端固定在O点的轻质弹簧连接组成弹簧振子.开始时,弹簧处于自然长度,导体棒MN具有水平向左的初速度v0,经过一段时间,导体棒MN第一次运动到最右端,这一过程中A、B间的电阻R上产生的焦耳热为Q,已知运动过程中MN始终与AD、BC垂直,则( )
如图所示,ABCD为固定的水平光滑矩形金属导轨,处在方向竖直向下,磁感应强度为B的匀强磁场中,A、B间距为L,左右两端均接有阻值为R的电阻,质量为m、长为L且不计电阻的导体棒MN放在导轨上,与导轨接触良好,与左端固定在O点的轻质弹簧连接组成弹簧振子.开始时,弹簧处于自然长度,导体棒MN具有水平向左的初速度v0,经过一段时间,导体棒MN第一次运动到最右端,这一过程中A、B间的电阻R上产生的焦耳热为Q,已知运动过程中MN始终与AD、BC垂直,则( )
 如图所示,ABCD为固定的水平光滑矩形金属导轨,处在方向竖直向下,磁感应强度为B的匀强磁场中,A、B间距为L,左右两端均接有阻值为R的电阻,质量为m、长为L且不计电阻的导体棒MN放在导轨上,与导轨接触良好,与左端固定在O点的轻质弹簧连接组成弹簧振子.开始时,弹簧处于自然长度,导体棒MN具有水平向左的初速度v0,经过一段时间,导体棒MN第一次运动到最右端,这一过程中A、B间的电阻R上产生的焦耳热为Q,已知运动过程中MN始终与AD、BC垂直,则( )
如图所示,ABCD为固定的水平光滑矩形金属导轨,处在方向竖直向下,磁感应强度为B的匀强磁场中,A、B间距为L,左右两端均接有阻值为R的电阻,质量为m、长为L且不计电阻的导体棒MN放在导轨上,与导轨接触良好,与左端固定在O点的轻质弹簧连接组成弹簧振子.开始时,弹簧处于自然长度,导体棒MN具有水平向左的初速度v0,经过一段时间,导体棒MN第一次运动到最右端,这一过程中A、B间的电阻R上产生的焦耳热为Q,已知运动过程中MN始终与AD、BC垂直,则( )| A. | 初始时刻棒所受的安培力大小为$\frac{2{B}^{2}{L}^{2}{v}_{0}}{R}$ | |
| B. | 当棒第一次到达最左端时,弹簧具有的弹性势能为$\frac{1}{2}$mv02-Q | |
| C. | 当棒第一次到达最右端时,弹簧具有的弹性势能为$\frac{1}{2}$mv02-2Q | |
| D. | 当棒第二次回到初始位置时,A、B间电阻的热功率为$\frac{2{B}^{2}{L}^{2}{v}_{0}^{2}}{R}$ |
6.某同学用如图1所示的装置探究加速度与力和质量的关系:
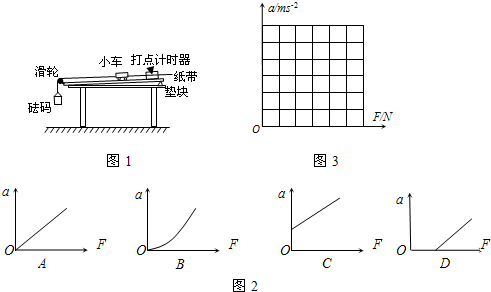
(1)某同学在平衡摩擦力时把木板的一端垫得过高,所得的a-F图象为图2中的C;
(2)某同学以砝码的重力为F,保持小车的质量不变,改变小盘和钩码的总质量,测得小车的加速度a和拉力F的数据如表所示
①根据表中的数据在如图3所示的坐标图上作出a-F图象
②通过计算小车的质量为1 kg;小车质量的计算值与实际值相比偏小(填“偏大”、“偏小”或“不变”)

(1)某同学在平衡摩擦力时把木板的一端垫得过高,所得的a-F图象为图2中的C;
(2)某同学以砝码的重力为F,保持小车的质量不变,改变小盘和钩码的总质量,测得小车的加速度a和拉力F的数据如表所示
| F (N) | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| a (m/s2) | 0.11 | 0.19 | 0.29 | 0.40 | 0.51 |
②通过计算小车的质量为1 kg;小车质量的计算值与实际值相比偏小(填“偏大”、“偏小”或“不变”)
16.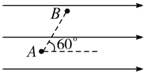 如图所示,A、B两点相距l=10cm,它们的连线与匀强电场场强方向夹角60°,把电子从A点移到B点,需克服电场力做功3.2×10-18J,则匀强电场的场强等于( )
如图所示,A、B两点相距l=10cm,它们的连线与匀强电场场强方向夹角60°,把电子从A点移到B点,需克服电场力做功3.2×10-18J,则匀强电场的场强等于( )
 如图所示,A、B两点相距l=10cm,它们的连线与匀强电场场强方向夹角60°,把电子从A点移到B点,需克服电场力做功3.2×10-18J,则匀强电场的场强等于( )
如图所示,A、B两点相距l=10cm,它们的连线与匀强电场场强方向夹角60°,把电子从A点移到B点,需克服电场力做功3.2×10-18J,则匀强电场的场强等于( )| A. | 800 N/C | B. | 400 N/C | C. | 400$\sqrt{3}$N/C | D. | 800$\sqrt{3}$N/C |
1.在如图所示的电路中,通过R1的电流I1是( )
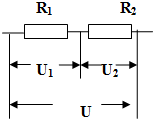

| A. | $\frac{U}{{R}_{1}}$ | B. | $\frac{{U}_{1}}{{R}_{1}}$ | C. | $\frac{{U}_{2}}{{R}_{2}}$ | D. | $\frac{U}{({R}_{1}+{R}_{2})}$ |
 如图所示,用与水平方向成θ角向上的推力F,将重为G的物体压在竖直的墙上,使之顺墙壁向上做匀速直线运动,求物体受到墙对它的弹力和摩擦力.
如图所示,用与水平方向成θ角向上的推力F,将重为G的物体压在竖直的墙上,使之顺墙壁向上做匀速直线运动,求物体受到墙对它的弹力和摩擦力. 如图,物体质量为2kg,静置于水平面上,它与水平面间的动摩擦因数为0.5,用大小为20N、方向与水平方向成37°的恒力F拉动物体,物体运动5s后撤去力F,到物体最后停下来,g取10m/s2.求:
如图,物体质量为2kg,静置于水平面上,它与水平面间的动摩擦因数为0.5,用大小为20N、方向与水平方向成37°的恒力F拉动物体,物体运动5s后撤去力F,到物体最后停下来,g取10m/s2.求: