题目内容
1. 质量为m,带电量为-q的粒子(不计重力),在匀强电场中的A点以初速度v0沿垂直于场强E的方向射入到电场中,已知粒子到达B点时的速度大小为2v0,A、B间距为d,如图所示.则A、B两点间的电势差为-$\frac{3m{v}_{0}^{2}}{2q}$;匀强电场的场强大小为$\frac{\sqrt{21}m{v}_{0}^{2}}{2qd}$,方向为向左.
质量为m,带电量为-q的粒子(不计重力),在匀强电场中的A点以初速度v0沿垂直于场强E的方向射入到电场中,已知粒子到达B点时的速度大小为2v0,A、B间距为d,如图所示.则A、B两点间的电势差为-$\frac{3m{v}_{0}^{2}}{2q}$;匀强电场的场强大小为$\frac{\sqrt{21}m{v}_{0}^{2}}{2qd}$,方向为向左.
分析 微粒重力不计,只受电场力作用,根据动能定理求解A、B两点间电压.
将微粒的运动分解为水平方向和竖直方向,竖直方向做匀速直线运动,水平方向做匀加速直线运动,分别列出两个方向的分位移,求出运动时间,再AB两点沿电场方向的距离,求解电场强度的大小.
解答 解:根据动能定理得:
-qUAB=$\frac{1}{2}m(2{v}_{0})^{2}-\frac{1}{2}m{v}_{0}^{2}$
得:UAB=-$\frac{3m{v}_{0}^{2}}{2q}$
微粒在B水平方向的分速度大小为:vx=$\sqrt{(2{v}_{0})^{2}-{v}_{0}^{2}}=\sqrt{3}{v}_{0}$
设A、B间水平距离为x,竖直距离为y.
水平方向微粒做匀加速直线运动,则有:
x=$\frac{{v}_{x}t}{2}$=$\frac{\sqrt{3}{v}_{0}t}{2}$
竖直方向微粒做匀速直线运动,则有:
y=vt
又d2=x2+y2
联立上述三式得:t=$\frac{2\sqrt{7}}{7}•\frac{d}{{v}_{0}}$
x=$\frac{{v}_{x}t}{2}$=$\frac{\sqrt{3}{v}_{0}t}{2}$=$\frac{\sqrt{21}}{7}d$
则电场强度为:E=$\frac{{U}_{AB}}{x}$=$\frac{\sqrt{21}m{v}_{0}^{2}}{2qd}$,方向向左;
故答案为:-$\frac{3m{v}_{0}^{2}}{2q}$,$\frac{\sqrt{21}m{v}_{0}^{2}}{2qd}$;向左.
点评 本题是类平抛运动,采用运动的合成与分解法,要抓住两个分运动的等时性.中等难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 在光滑水平面上有一质量为m的物块受到水平恒力F的作用而运动,在其正前方固定一个足够长的劲度系数为k的轻质弹簧,如图所示.当物块与弹簧接触且向右运动的过程中,下列说法正确的是( )
在光滑水平面上有一质量为m的物块受到水平恒力F的作用而运动,在其正前方固定一个足够长的劲度系数为k的轻质弹簧,如图所示.当物块与弹簧接触且向右运动的过程中,下列说法正确的是( )
 在光滑水平面上有一质量为m的物块受到水平恒力F的作用而运动,在其正前方固定一个足够长的劲度系数为k的轻质弹簧,如图所示.当物块与弹簧接触且向右运动的过程中,下列说法正确的是( )
在光滑水平面上有一质量为m的物块受到水平恒力F的作用而运动,在其正前方固定一个足够长的劲度系数为k的轻质弹簧,如图所示.当物块与弹簧接触且向右运动的过程中,下列说法正确的是( )| A. | 物块在接触弹簧的过程中一直做减速运动 | |
| B. | 物块接触弹簧后先加速后减速,当弹力等于F时其速度最大 | |
| C. | 当弹簧处于压缩量最大时,物块的加速度等于$\frac{F}{m}$ | |
| D. | 当物块的速度为零时,弹簧的压缩量等于$\frac{F}{k}$ |
9.一宇宙飞船绕地心做半径为r的匀速圆周运动,飞船舱内有一质量为m的人站在可称体重的台秤上,用R表示地球的半径,g表示地球表面处的重力加速度,g′表示宇宙飞船所在处的地球引力加速度,N表示人对秤的压力,下面说法正确的是( )
| A. | N=0 | B. | g′=$\frac{{R}^{2}}{{r}^{2}}$g | C. | g′=0 | D. | N=m$\frac{R}{r}$g |
13.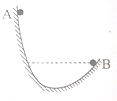 如图所示,一物块以速度v1从曲面上A点处下滑,运动到B点处速度大小仍为v1,若物块以速度v2(v2>v1)仍从A点下滑,则运动到B点时速度的大小将( )
如图所示,一物块以速度v1从曲面上A点处下滑,运动到B点处速度大小仍为v1,若物块以速度v2(v2>v1)仍从A点下滑,则运动到B点时速度的大小将( )
 如图所示,一物块以速度v1从曲面上A点处下滑,运动到B点处速度大小仍为v1,若物块以速度v2(v2>v1)仍从A点下滑,则运动到B点时速度的大小将( )
如图所示,一物块以速度v1从曲面上A点处下滑,运动到B点处速度大小仍为v1,若物块以速度v2(v2>v1)仍从A点下滑,则运动到B点时速度的大小将( )| A. | 稍大于v2 | B. | 稍小于v2 | C. | 等于v2 | D. | 稍小于v1 |
5.以下说法正确的是( )
| A. | 第一宇宙速度是人造地球卫星绕地球飞行的最小速度 | |
| B. | 第二宇宙速度是使卫星脱离地球引力的最小发射速度 | |
| C. | 第三宇宙速度是使卫星脱离地球引力的最小发射速度 | |
| D. | 第一宇宙速度是使人造地球卫星绕地球飞行的最大发射速度 |
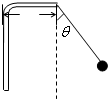 如图所示,已知绳长L=1m,水平杆长S=0.6m,小球质量m=0.5kg,整个装置可绕竖直轴转动.(sin37°=0.6,cos37°=0.8)
如图所示,已知绳长L=1m,水平杆长S=0.6m,小球质量m=0.5kg,整个装置可绕竖直轴转动.(sin37°=0.6,cos37°=0.8)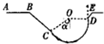 滑板极限运动场地如图所示,滑道AB水平,长s=5m,BC倾斜,CD为竖直平面内半径R=1.0m的光滑贺弧轨道,圆心O与C的连线与竖直方向的夹角α=53°,D的切线方向竖直,一个质量m=60kg(包括滑板)运动员从A点由静止出发,经B点飞出,恰好从C点的切线方向进入圆形滑道,再从D点竖直向上运动到达最高点E.已知E点相对圆弧滑道最低点的高度H=2.2m,已知重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6.(空气阻力不计)
滑板极限运动场地如图所示,滑道AB水平,长s=5m,BC倾斜,CD为竖直平面内半径R=1.0m的光滑贺弧轨道,圆心O与C的连线与竖直方向的夹角α=53°,D的切线方向竖直,一个质量m=60kg(包括滑板)运动员从A点由静止出发,经B点飞出,恰好从C点的切线方向进入圆形滑道,再从D点竖直向上运动到达最高点E.已知E点相对圆弧滑道最低点的高度H=2.2m,已知重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6.(空气阻力不计)