题目内容
11.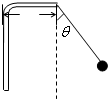 如图所示,已知绳长L=1m,水平杆长S=0.6m,小球质量m=0.5kg,整个装置可绕竖直轴转动.(sin37°=0.6,cos37°=0.8)
如图所示,已知绳长L=1m,水平杆长S=0.6m,小球质量m=0.5kg,整个装置可绕竖直轴转动.(sin37°=0.6,cos37°=0.8)求:(1)要使绳子与竖直方向成37°,试求该装置必须以多大角速度转动才行?
(2)此时绳的张力是多大?
分析 (1)小球受重力和拉力,靠两个力的合力提供向心力,根据牛顿第二定律求出该装置的角速度.
(2)根据平行四边形定则求出绳子对小球的拉力.
解答  解:(1)根据牛顿第二定律得,mgtanθ=mrω2
解:(1)根据牛顿第二定律得,mgtanθ=mrω2
r=b+asinθ=0.6+1×0.6m=1.2m
则角速度ω=$\sqrt{\frac{gtanθ}{r}}=\sqrt{\frac{10×\frac{3}{4}}{1.2}}rad/s=2.5rad/s$.
(2)根据平行四边形定则得,绳子对小球的拉力$F=\frac{mg}{cos37°}=\frac{0.5×10}{0.8}N=6.25N$.
答:(1)该装置必须以2.5rad/s的角速度旋转.
(2)绳子对小球的拉力大小为6.25N.
点评 解决本题的关键知道小球做圆周运动向心力的来源,结合牛顿第二定律进行求解.

练习册系列答案
相关题目
1.从某一高度相隔1s释放两个相同的小球甲和乙,不计空气阻力,它们在落地前( )
| A. | 甲、乙两球距离越来越大,但甲、乙两球速度之差保持不变 | |
| B. | 甲、乙两球距离越来越大,且甲、乙两球速度之差越来越大 | |
| C. | 甲、乙两球距离始终保持不变,且甲、乙两球速度之差保持不变 | |
| D. | 甲、乙两球距离越来越小,且甲、乙两球速度之差越来越小 |
2.下列说法中正确的是( )
| A. | 在三峡高中16届田径运动会中,运动员跑完200m位移的大小和路程不相等 | |
| B. | 三峡高中12:50学生开始午休,其中“12:50”指的是时间 | |
| C. | 平均速率等于平均速度的大小 | |
| D. | 速率为瞬时速度的大小,速度是标量 |
19.下列关于物体的动能的叙述中,正确的是( )
| A. | 速度不变、运动物体的质量发生变化,它的动能一定也变化 | |
| B. | 质量不变、运动物体的速度发生变化,它的动能一定也变化 | |
| C. | 速度减半,质量增大到原来的4倍,物体的动能是原来的2倍 | |
| D. | 质量减半,速度增大到原来的2倍,物体的动能是原来的4倍 |
6.在电磁学发展过程中,许多科学家做出了贡献,下列说法正确的是( )
| A. | 奥斯特发现了电流磁效应;法拉第发现了电磁感应现象 | |
| B. | 麦克斯韦预言了电磁波;楞次用实验证实了电磁波的存在 | |
| C. | 法拉第发现了点电荷的相互作用规律;密立根通过油滴实验测定了元电荷的数值 | |
| D. | 安培发现了磁场对运动电荷的作用规律;洛伦兹发现了磁场对电流的作用规律 |
16.传感器担负着信息采集的任务,它常常不用于下列哪种情况( )
| A. | 将力学量(如形变量)转变成电学量 | B. | 将热学量转变成电学量 | ||
| C. | 将光学量转变成电学量 | D. | 将电学量转变成力学量 |
3.关于地球同步通信卫星,下列说法中正确的是( )
| A. | 它的发射速度不可能小于7.9km/s | |
| B. | 已知它的质量是1.42T,若将它的质量增为2.84T,其同步轨道的半径变为原来的2倍 | |
| C. | 它可以绕过成都的正上方,所以可以利用它转播四川电视台的节目 | |
| D. | 它距地面的高度约是地球半径的5倍,所以它的向心加速度约是地面处的重力加速度的$\frac{1}{25}$ |
 计算机上常用的“3.5英寸、1.44MB”软磁盘的磁道和扇区如图所示,磁盘上共有80个磁道(即80个不同半径的同心圆),每 个磁道分成18个扇区(每个扇区为$\frac{1}{18}$圆周),每个扇区可记 录512个字节.电动机使磁盘以300r/min匀速转动.磁头在读、写数据时是不动的.磁盘每转一圈,磁头沿半径方向跳动一个磁道.则一个扇区通过磁头所用的时间是$\frac{1}{90}$s.
计算机上常用的“3.5英寸、1.44MB”软磁盘的磁道和扇区如图所示,磁盘上共有80个磁道(即80个不同半径的同心圆),每 个磁道分成18个扇区(每个扇区为$\frac{1}{18}$圆周),每个扇区可记 录512个字节.电动机使磁盘以300r/min匀速转动.磁头在读、写数据时是不动的.磁盘每转一圈,磁头沿半径方向跳动一个磁道.则一个扇区通过磁头所用的时间是$\frac{1}{90}$s. 质量为m,带电量为-q的粒子(不计重力),在匀强电场中的A点以初速度v0沿垂直于场强E的方向射入到电场中,已知粒子到达B点时的速度大小为2v0,A、B间距为d,如图所示.则A、B两点间的电势差为-$\frac{3m{v}_{0}^{2}}{2q}$;匀强电场的场强大小为$\frac{\sqrt{21}m{v}_{0}^{2}}{2qd}$,方向为向左.
质量为m,带电量为-q的粒子(不计重力),在匀强电场中的A点以初速度v0沿垂直于场强E的方向射入到电场中,已知粒子到达B点时的速度大小为2v0,A、B间距为d,如图所示.则A、B两点间的电势差为-$\frac{3m{v}_{0}^{2}}{2q}$;匀强电场的场强大小为$\frac{\sqrt{21}m{v}_{0}^{2}}{2qd}$,方向为向左.