题目内容
(1)下列说法正确的是______A.地面附近有一高速水平飞过的火箭,地面上的人观察到的“火箭长度”要比火箭上的人观察到的“火箭长度”短一些
B.拍摄玻璃橱窗内的物品时,往往在镜头前加一个偏振片以增加透射光的强度
C.变化的电场一定产生变化的磁场;变化的磁场一定产生变化的电场
D.单摆在周期性外力作用下做受迫振动,其振动周期与单摆的摆长有关
E.次声波是频率低于20Hz的声波;它比超声波更易发生衍射
F.一列加速驶出车站的火车,站台上的人听到汽笛音调变高了

(2)空间中存在一列向右传播的简谐横波,波速为2m/s,在t=0时刻的波形如图(1)所示.试写出x=2.0m处质点的位移--时间关系表达式______;若空间中存在振幅不同,波速相同的两列机械波相向传播,它们的周期均为T,t=0时刻两列波的波形如图(2)所示,请定性画出
 时刻的波形图.
时刻的波形图.(3)如图(3)所示,置于空气中的一不透明容器内盛满某种透明液体,容器高为6.0cm,其底部紧靠器壁处有一竖直放置的3.0cm长的线光源,顶部一部分开口,另一部分封闭,封闭部分的内表面涂有8.0cm长的吸光物质(光线射到吸光物质上,会被全部吸收),靠近容器右端有一水平放置的与液面等高的望远镜用来观察线光源,此时通过望远镜恰好只能看到线光源的底端.求此液体的折射率n.
【答案】分析:(1)A.根据相对论效应,分析地面上的人观察到的“火箭长度”与火箭上的人观察到的“火箭长度”关系.拍摄玻璃橱窗内的物品时,往往在镜头前加一个偏振片以减弱反射光的强度.变化的电场不一定产生变化的磁场;变化的磁场也不一定产生变化的电场.单摆在周期性外力作用下做受迫振动,其振动周期等于驱动力的频率.次声波的波长比超声波的波长长,更容.易发生衍射.一列加速驶出车站的火车,站台上的人听到汽笛音调变低了.
(2)由波形图读出振幅和波长,求出周期,再求角频率.写出x=2.0m处质点的位移--时间关系表达式.根据波传播的距离,分析波叠加的结果.
(3)由题,通过望远镜恰好只能看到线光源的底端,则线光源底端发出光射到吸光物质的最右边时恰好发生全反射,根据几何知识求出临界角,再求解折射率.
解答: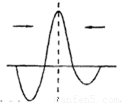 解:
解:
(1)A、根据相对论“尺缩效应”可知,地面上的人观察到的“火箭长度”要比火箭上的人观察到的“火箭长度”短一些.故A正确.
B、拍摄玻璃橱窗内的物品时,往往在镜头前加一个偏振片是为了将玻璃的反射光减弱.故B错误,使相片清晰.故B错误.
C、根据麦克斯韦电磁场理论得知,变化的电场一定产生磁场,但不一定产生变化的磁场;变化的磁场一定产生电场,但不一定产生变化的电场;故C错误.
D、单摆在周期性外力作用下做受迫振动,其振动周期等于驱动力的周期,与单摆的摆长无关.故D错误.
E、次声波的频率小于超声波的频率,波长比超声波长,更易发生衍射.故E正确.
F、一列加速驶出车站的火车,离站台上的人的距离增大了,根据多普勒效应得知,站台上的人听到汽笛音调变低了.故F错误.
故选AE
(2)由图读出振幅A=5cm,波长λ=2m,则周期T=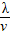 =
=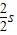 ,角频率ω=
,角频率ω=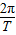 =2πrad/s.波向右传播,图示时刻x=2.0m处质点振动方向沿y轴负方向,则x=2.0m处质点的位移--时间关系表达式为y=-5sinωt(cm)=-5sin2πtcm.在
=2πrad/s.波向右传播,图示时刻x=2.0m处质点振动方向沿y轴负方向,则x=2.0m处质点的位移--时间关系表达式为y=-5sinωt(cm)=-5sin2πtcm.在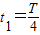 时刻,两列波的波峰在虚线处相遇,振幅等于两列波振幅之和,画出波形如图.
时刻,两列波的波峰在虚线处相遇,振幅等于两列波振幅之和,画出波形如图.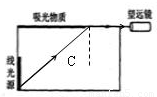
(3)由题意: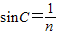 ,又由几何知识得,sinC=
,又由几何知识得,sinC= =
=
解得:n=1.25
故答案为:
(1)AE
(2)y=-5sin2πtcm,波形如图.
(3)此液体的折射率n=1.25.
点评:本题是高考选修部分的考试模式,这部分没有难题,立足基础,紧扣书本,是学习的基本策略.
(2)由波形图读出振幅和波长,求出周期,再求角频率.写出x=2.0m处质点的位移--时间关系表达式.根据波传播的距离,分析波叠加的结果.
(3)由题,通过望远镜恰好只能看到线光源的底端,则线光源底端发出光射到吸光物质的最右边时恰好发生全反射,根据几何知识求出临界角,再求解折射率.
解答:
 解:
解:(1)A、根据相对论“尺缩效应”可知,地面上的人观察到的“火箭长度”要比火箭上的人观察到的“火箭长度”短一些.故A正确.
B、拍摄玻璃橱窗内的物品时,往往在镜头前加一个偏振片是为了将玻璃的反射光减弱.故B错误,使相片清晰.故B错误.
C、根据麦克斯韦电磁场理论得知,变化的电场一定产生磁场,但不一定产生变化的磁场;变化的磁场一定产生电场,但不一定产生变化的电场;故C错误.
D、单摆在周期性外力作用下做受迫振动,其振动周期等于驱动力的周期,与单摆的摆长无关.故D错误.
E、次声波的频率小于超声波的频率,波长比超声波长,更易发生衍射.故E正确.
F、一列加速驶出车站的火车,离站台上的人的距离增大了,根据多普勒效应得知,站台上的人听到汽笛音调变低了.故F错误.
故选AE
(2)由图读出振幅A=5cm,波长λ=2m,则周期T=
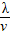 =
=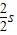 ,角频率ω=
,角频率ω=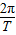 =2πrad/s.波向右传播,图示时刻x=2.0m处质点振动方向沿y轴负方向,则x=2.0m处质点的位移--时间关系表达式为y=-5sinωt(cm)=-5sin2πtcm.在
=2πrad/s.波向右传播,图示时刻x=2.0m处质点振动方向沿y轴负方向,则x=2.0m处质点的位移--时间关系表达式为y=-5sinωt(cm)=-5sin2πtcm.在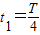 时刻,两列波的波峰在虚线处相遇,振幅等于两列波振幅之和,画出波形如图.
时刻,两列波的波峰在虚线处相遇,振幅等于两列波振幅之和,画出波形如图.
(3)由题意:
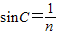 ,又由几何知识得,sinC=
,又由几何知识得,sinC= =
=
解得:n=1.25
故答案为:
(1)AE
(2)y=-5sin2πtcm,波形如图.
(3)此液体的折射率n=1.25.
点评:本题是高考选修部分的考试模式,这部分没有难题,立足基础,紧扣书本,是学习的基本策略.

练习册系列答案
相关题目
 (1)下列说法正确的是
(1)下列说法正确的是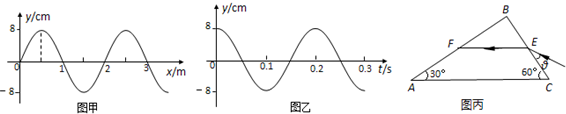

 (1)下列说法正确的是
(1)下列说法正确的是 (1)下列说法正确的是( )
(1)下列说法正确的是( )