题目内容
如图所示,在倾角为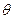 的光滑斜面上,存在着两个磁感应强度相等的匀强磁场,方向一个垂直斜面向上,另一个垂直斜面向下,宽度均为L,一个质量为m,边长为L的正方形线框以速度v刚进入上边磁场时,即恰好做匀速直线运动,求:
的光滑斜面上,存在着两个磁感应强度相等的匀强磁场,方向一个垂直斜面向上,另一个垂直斜面向下,宽度均为L,一个质量为m,边长为L的正方形线框以速度v刚进入上边磁场时,即恰好做匀速直线运动,求:
(1)当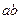 边刚越过
边刚越过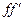 时,线框的加速度多大?方向如何?
时,线框的加速度多大?方向如何?
(2)当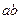 到达
到达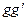 与
与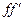 中间位置时,线框又恰好作匀速运动,求线框从开始进入到
中间位置时,线框又恰好作匀速运动,求线框从开始进入到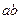 边到达
边到达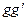 与
与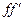 中间位置时,产生的热量是多少?
中间位置时,产生的热量是多少?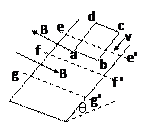
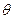 的光滑斜面上,存在着两个磁感应强度相等的匀强磁场,方向一个垂直斜面向上,另一个垂直斜面向下,宽度均为L,一个质量为m,边长为L的正方形线框以速度v刚进入上边磁场时,即恰好做匀速直线运动,求:
的光滑斜面上,存在着两个磁感应强度相等的匀强磁场,方向一个垂直斜面向上,另一个垂直斜面向下,宽度均为L,一个质量为m,边长为L的正方形线框以速度v刚进入上边磁场时,即恰好做匀速直线运动,求:(1)当
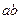 边刚越过
边刚越过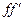 时,线框的加速度多大?方向如何?
时,线框的加速度多大?方向如何?(2)当
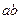 到达
到达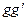 与
与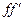 中间位置时,线框又恰好作匀速运动,求线框从开始进入到
中间位置时,线框又恰好作匀速运动,求线框从开始进入到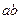 边到达
边到达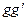 与
与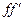 中间位置时,产生的热量是多少?
中间位置时,产生的热量是多少?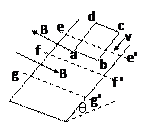
⑴a=3gsinθ,方向沿斜面向上
(2)Q=1/2mv02+2mgsinθ-1/2mvx2 =3mgLsinθ/2 +15 mv2/32
(2)Q=1/2mv02+2mgsinθ-1/2mvx2 =3mgLsinθ/2 +15 mv2/32
⑴当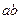 边刚越过
边刚越过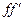 时,回路中的感应电动势为:E=2BLv
时,回路中的感应电动势为:E=2BLv
回路中的电流为:I= ,线框所受的安培力为:FA=2BIL=4B2L2v/R
,线框所受的安培力为:FA=2BIL=4B2L2v/R
根据力的平衡有: ,由此可得:FA=
,由此可得:FA=
根据牛顿第二定律有:ma=4mgsinθ-mgsinθ
解得:a=3gsinθ,方向沿斜面向上
(2)此时的速度为vx ,由力的平衡有: ,解得:vx=
,解得:vx=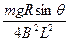
根据能的转化与守恒定律得: 1/2mvx2+Q=1/2mv02+2mgLsinθ
解得:Q=1/2mv02+2mgsinθ-1/2mvx2 =3mgLsinθ/2 +15 mv2/32
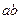 边刚越过
边刚越过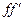 时,回路中的感应电动势为:E=2BLv
时,回路中的感应电动势为:E=2BLv回路中的电流为:I=
 ,线框所受的安培力为:FA=2BIL=4B2L2v/R
,线框所受的安培力为:FA=2BIL=4B2L2v/R根据力的平衡有:
 ,由此可得:FA=
,由此可得:FA=
根据牛顿第二定律有:ma=4mgsinθ-mgsinθ
解得:a=3gsinθ,方向沿斜面向上
(2)此时的速度为vx ,由力的平衡有:
 ,解得:vx=
,解得:vx=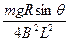
根据能的转化与守恒定律得: 1/2mvx2+Q=1/2mv02+2mgLsinθ
解得:Q=1/2mv02+2mgsinθ-1/2mvx2 =3mgLsinθ/2 +15 mv2/32

练习册系列答案
相关题目
 的虚线的上方有一个方向垂直于纸面水平向里的匀强磁场,磁感应强度B=1T。正方形线框
的虚线的上方有一个方向垂直于纸面水平向里的匀强磁场,磁感应强度B=1T。正方形线框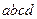 的边长
的边长 =0.2m、质量m=0.1kg,R=0.08Ω,物体A的质量M=0.2kg。开始时线框的
=0.2m、质量m=0.1kg,R=0.08Ω,物体A的质量M=0.2kg。开始时线框的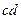 边在地面上,各段绳都处于伸直状态,从如图所示的位置将A从静止释放。一段时间后线框进入磁场运动。当线框的
边在地面上,各段绳都处于伸直状态,从如图所示的位置将A从静止释放。一段时间后线框进入磁场运动。当线框的
 可在导轨上
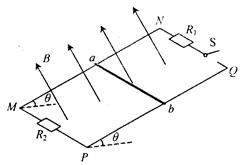
可在导轨上 无摩擦地滑动。棒与导轨垂直,并接触良好。导轨之间有垂直纸面向外的匀强磁场,磁感强度为B。导轨右边与电路连接。电路中的两个定值电阻组织分别为2R和R。在BD间接有一水平放置的平行板电容器C,板间距离为d。当
无摩擦地滑动。棒与导轨垂直,并接触良好。导轨之间有垂直纸面向外的匀强磁场,磁感强度为B。导轨右边与电路连接。电路中的两个定值电阻组织分别为2R和R。在BD间接有一水平放置的平行板电容器C,板间距离为d。当
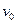 匀速向左运动时,电容器中质量为m的带电微粒恰好静止。求:微粒的带电性质,及带电量的大小。
匀速向左运动时,电容器中质量为m的带电微粒恰好静止。求:微粒的带电性质,及带电量的大小。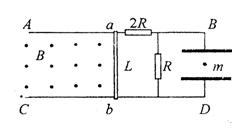


 ”形的金属槽放置在磁感应强度为B的匀强磁场中,并以速度v1向右匀速运动,从槽口右侧射入的带电微粒的速度是v2,如果微粒进入槽后恰能做匀速圆周运动,则微粒做匀速圆周运动的轨道半径r和周期T分别为( )
”形的金属槽放置在磁感应强度为B的匀强磁场中,并以速度v1向右匀速运动,从槽口右侧射入的带电微粒的速度是v2,如果微粒进入槽后恰能做匀速圆周运动,则微粒做匀速圆周运动的轨道半径r和周期T分别为( )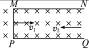
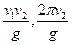

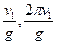
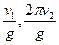
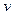
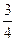
 、
、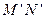 和
和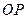 、
、 间距都是
间距都是 ,二者之间固定有两组竖直半圆形轨道
,二者之间固定有两组竖直半圆形轨道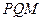 和
和 ,两轨道间距也均为
,两轨道间距也均为 端、
端、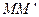 端的对接狭缝宽度可忽略不计,图中的虚线为绝缘材料制成的固定支架,能使导轨系统位置固定。将一质量为
端的对接狭缝宽度可忽略不计,图中的虚线为绝缘材料制成的固定支架,能使导轨系统位置固定。将一质量为 的金属杆沿垂直导轨方向放在下层导轨的最左端
的金属杆沿垂直导轨方向放在下层导轨的最左端 位置,金属杆在与水平成
位置,金属杆在与水平成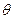 角斜向上的恒力作用下沿导轨运动,运动过程中金属杆始终与导轨垂直,且接触良好。当金属杆通过4R的距离运动到导轨末端
角斜向上的恒力作用下沿导轨运动,运动过程中金属杆始终与导轨垂直,且接触良好。当金属杆通过4R的距离运动到导轨末端 位置时其速度大小
位置时其速度大小 。金属杆和导轨的电阻、金属杆在半圆轨道和上层水平导轨上运动过程中所受的摩擦阻力,以及整个运动过程中所受空气阻力均可忽略不计。
。金属杆和导轨的电阻、金属杆在半圆轨道和上层水平导轨上运动过程中所受的摩擦阻力,以及整个运动过程中所受空气阻力均可忽略不计。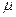 ,求金属杆所受恒力F的大小;
,求金属杆所受恒力F的大小; 和
和 ,又在对接狭缝
,又在对接狭缝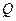 和
和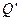 处无碰撞地水平进入第二组半圆形轨道
处无碰撞地水平进入第二组半圆形轨道 和
和 的内侧,求金属杆运动到半圆轨道的最高位置
的内侧,求金属杆运动到半圆轨道的最高位置 其右端连接的定值电阻阻值为
其右端连接的定值电阻阻值为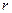 ,导轨处于磁感应强度为B、方向竖直
,导轨处于磁感应强度为B、方向竖直 向下的匀强磁场中。金属杆由第二组半圆轨道的最高位置
向下的匀强磁场中。金属杆由第二组半圆轨道的最高位置