题目内容
13.一静止的${\;}_{92}^{238}U$核经α衰变成为${\;}_{90}^{234}Th$核,释放出的总动能为4.27MeV.问此衰变后${\;}_{90}^{234}Th$核的动能为多少MeV(保留1位有效数字)?分析 选择正确的研究对象.根据动量守恒定律列出等式解决问题,根据能量守恒列出等式求解问题.
解答 解:据题意知,此α衰变的方程为${\;}_{92}^{238}U→{\;}_{90}^{234}Th+{\;}_2^4He$
根据动量守恒定律得mαvα=mThvTh ①
式中,mα和mTh分别为α粒子和Th核的质量,vα和vTh分别为α粒子和Th核的速度的大小.由题设条件知$\frac{1}{2}{m_a}v_a^2+\frac{1}{2}{m_{Th}}v_{Th}^2={E_k}$②
$\frac{m_a}{{{m_{Th}}}}=\frac{4}{234}$③
式中Ek=4.27MeV是α粒子与Th的总动能.
由①②③式得$\frac{1}{2}{m_{Th}}v_{Th}^2=\frac{m_a}{{{m_a}+{m_{Th}}}}{E_k}$④
代入数据得,衰变后${\;}_{90}^{234}Th$核的动能$\frac{1}{2}{m_{Th}}v_{Th}^2=0.07MeV$⑤
答:衰变后${\;}_{90}^{234}Th$核的动能为0.07MeV.
点评 解决问题首先要清楚研究对象的运动过程.我们要清楚运动过程中能量的转化,以便从能量守恒角度解决问题.把动量守恒和能量守恒结合起来列出等式求解是常见的问题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
4.物体在万有引力场中具有的势能叫做引力势能.若取两物体相距无穷远时的引力势能为零,一个质量为m0的质点距质量为M0的引力中心为r0时,其万有引力势能可表示为:Ep=-G$\frac{{M}_{0}{m}_{0}}{{r}_{0}}$(式中G为引力常数).一颗质量为m的人造地球卫星以半径为r1圆形轨道环绕地球飞行,已知地球的质量为M,要使此卫星绕地球做匀速圆周运动的轨道半径增大为r2,则在此过程中( )
| A. | 卫星势能增加了GMm($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$) | |
| B. | 卫星动能减少了G$\frac{Mm}{3}$($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$) | |
| C. | 卫星机械能增加了G$\frac{Mm}{2}$($\frac{1}{{r}_{1}}$+$\frac{1}{{r}_{2}}$) | |
| D. | 卫星上的发动机所消耗的最小能量为G$\frac{2Mm}{3}$($\frac{1}{{r}_{2}}$-$\frac{1}{{r}_{1}}$) |
8. 电阻R、电容C与一线圈连成闭合电路,条形磁铁静止于线圈的正上方,N极朝下,如图所示.现使磁铁开始自由下落,在N极接近线圈上端的过程中,流过R的电流方向和电容器极板的带电情况是( )
电阻R、电容C与一线圈连成闭合电路,条形磁铁静止于线圈的正上方,N极朝下,如图所示.现使磁铁开始自由下落,在N极接近线圈上端的过程中,流过R的电流方向和电容器极板的带电情况是( )
 电阻R、电容C与一线圈连成闭合电路,条形磁铁静止于线圈的正上方,N极朝下,如图所示.现使磁铁开始自由下落,在N极接近线圈上端的过程中,流过R的电流方向和电容器极板的带电情况是( )
电阻R、电容C与一线圈连成闭合电路,条形磁铁静止于线圈的正上方,N极朝下,如图所示.现使磁铁开始自由下落,在N极接近线圈上端的过程中,流过R的电流方向和电容器极板的带电情况是( )| A. | 从a到b | B. | 没有电流 | C. | 上极板带正电 | D. | 下极板带正电 |
18.在静电场中,有关电场线的一些说法,哪些是正确的( )
| A. | 初速度为零的点电荷,在电场中只受电场力作用,则它运动的轨迹可能与电场线重合 | |
| B. | 电场线通过的地方有电场,电场线不通过的地方无电场,它是静电场中客观存在的 | |
| C. | 点电荷在电场中受到的电场力方向,可能与电场线垂直 | |
| D. | 电场线从正电荷出发,到负电荷终止,中途不中断,不相交 |
2.在距地面高5m的平台上,以25m/s的速率竖直向上抛出一个质量为1kg的石块,不计空气阻力,则在抛出后第3秒内重力对石块所做的功为( )
| A. | -100J | B. | 50J | C. | 10J | D. | 0J |
3.做匀速圆周运动的物体,在运动过程中保持不变的物理量是( )
| A. | 动能 | B. | 速度 | C. | 加速度 | D. | 机械能 |
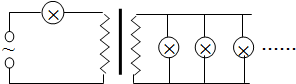 如图所示,交流发电机电动势的有效值为E=20V,内阻不计,它通过一个R=6Ω的指示灯连接降压变压器.降压变压器输出端并联24只彩色小灯泡,每只灯泡都是“6V、0.25W”,灯泡都正常发光,导线电阻不计.求:
如图所示,交流发电机电动势的有效值为E=20V,内阻不计,它通过一个R=6Ω的指示灯连接降压变压器.降压变压器输出端并联24只彩色小灯泡,每只灯泡都是“6V、0.25W”,灯泡都正常发光,导线电阻不计.求: 如图的电路中,电池组的电动势?=30伏特,电阻R2=10欧姆,两个水平放置的带电金属板间的距离d=15厘米.在金属板间的匀强电场中,有一质量为m=7×10-5克带电量q=-5×10-10库仑的油滴,当把可变电阻器R3的阻值调到35欧姆接入电路时,带电油滴恰好静止悬浮在电场中,此时安培表示数I=1.5安培,试g=10m/s2求:
如图的电路中,电池组的电动势?=30伏特,电阻R2=10欧姆,两个水平放置的带电金属板间的距离d=15厘米.在金属板间的匀强电场中,有一质量为m=7×10-5克带电量q=-5×10-10库仑的油滴,当把可变电阻器R3的阻值调到35欧姆接入电路时,带电油滴恰好静止悬浮在电场中,此时安培表示数I=1.5安培,试g=10m/s2求: 如图所示,是A、B两物体同时由同一地点向同一方向做直线运动的v-t图象,则B物体运动的加速度为0.25m/s2,经40s 物体A、B相遇.
如图所示,是A、B两物体同时由同一地点向同一方向做直线运动的v-t图象,则B物体运动的加速度为0.25m/s2,经40s 物体A、B相遇.