题目内容
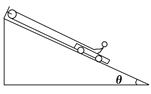
【题目】如图所示,在倾角为θ=30°的固定斜面上,跨过定滑轮的轻绳一端系在小车的前端,另一端被坐在小车上的人拉住.已知人的质量为60 kg,小车的质量为10 kg,绳及滑轮的质量、滑轮与绳间的摩擦均不计,斜面对小车的摩擦阻力为人和小车总重力的0.1倍,取重力加速度g=10 m/s2,当人以280 N的力拉绳时,试求(斜面足够长):
(1)人与车一起向上运动的加速度大小;
(2)人所受摩擦力的大小和方向;
(3)某时刻人和车沿斜面向上的速度为3 m/s,此时人松手,则人和车一起滑到最高点所用时间为多少?
【答案】(1)2 m/s2 (2)140 N,方向沿斜面向上 (3) 0.5 s
【解析】(1)对整体,设人的质量为m1,小车质量为m2,斜面对小车的摩擦力为f1=k(m1+m2)g,小车对人的静摩擦力为f2,绳子上的张力为F.则:
2F-(m1+m2)gsin30°-f1=(m1+m2)a,①
f1=k(m1+m2)g,②
解得a=2m/s2
故人与车一起运动的加速度大小为2 m/s2.方向沿斜面向上;
(2)对人受力分析知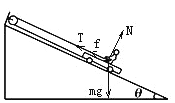
F-m1gsin30°+f2=m1a,
解得f2=140N,方向沿斜面向上
故人所受摩擦力的大小为140N,方向沿斜面向上.
(3)撤去拉力后,人和车共同加速度为:a1=gsin30°+0.1g=6m/s2;
人和车一起滑到最高点所用时间t=![]() =0.5s;
=0.5s;

【题目】(10分)在“描绘小灯泡的伏安特性曲线”的实验中,需测量一个标有“3V,1.5W”灯泡两端的电压和通过灯泡的电流。现有如下器材:
直流电源(电动势3.0V,内阻不计)
电流表A1(量程3A,内阻约0.1Ω) 电流表A2(量程600mA,内阻约5Ω)
电压表V1(量程3V,内阻约3kΩ) 电压表V2(量程15V,内阻约200kΩ)
滑动变阻器R1(阻值0 10Ω,额定电流1A)
滑动变阻器R2(阻值0 1kΩ,额定电流300mA)
①该实验中,电流表应选择 (填“A1”或“A2”),电压表应选择 (填“V1”或“V2”),滑动变阻器应选择 (填“R1”或“R2”)。
②某同学用导线a、b、c、d、e、f、g和h连接成如图甲所示的电路,请在方框中完成实验的电路图。

③ 下表是学习小组在实验中测出的6组数据,某同学根据表格中的数据在方格纸上已画出了5个数据的对应点,请你画出第4组数据的对应点,并作出该小灯泡的伏安特性曲线。
U(V) | I(A) | |
1 | 0 | 0 |
2 | 0.5 | 0.17 |
3 | 1.0 | 0.30 |
4 | 1.5 | 0.39 |
5 | 2.0 | 0.45 |
6 | 2.5 | 0.49 |

④ 若将该灯泡与一个6.0Ω的定值电阻串联,直接接在题中提供的电源两端,请估算该小灯泡的实际功率P= W(保留两位有效数字)。(若需作图,可直接画在第③小题图中)