Question

【题目】在水平桌面上画两个同心圆，它们的半径分别为r和2r。圆心处摆放一颗棋子B，大圆周上另一颗棋子A以某一初速度v0沿直径方向向右正对B运动，它们在圆心处发生弹性碰撞后，A刚好停在小圆周上，而B则刚好停在大圆周上。两颗棋子碰撞前后都在同一条直线上运动，它们与桌面间的动摩擦因数均为，棋子大小远小于圆周半径，重力加速度为g。试求

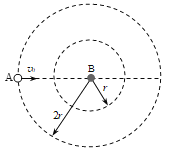
(1)A、B两颗棋子的质量之比。

(2)棋子A的初速度v0。

Answer 1

【答案】(1) (2)

【解析】

（1）AB碰撞时动量及能量守恒，分别对两物体列动能定理联立求解两物体的质量之比；

（2）根据动能定理求解棋子的初速度。

（1）设A、B质量分别为mA、mB，碰撞前、后A的速度分别是vA0、vA，碰撞后B的速度为vB。

由于是弹性碰撞，故有 ①

②

依题意碰后A停在小圆周上，根据动能定理有

③

而B停在大圆周上，则

④

先讨论 的情况。在此条件下，A停在圆心右侧的小圆周上，B停在圆心右侧大圆周上。联立①②③④解得 ⑤

与题设不符，故一定有⑥

因此，碰后A一定是反向运动，这样，A只可能停在圆心左侧的小圆周上。

根据①②③④⑥解得⑦

（2）根据动能定理，碰前对A有⑧

联立①③④⑥⑦⑧解得 ⑨