题目内容
(9分)27.如图,MN是一条通过透明球体球心的直线。在真空中波长为λ0=400 nm的单色细光束AB平行于MN的射向球体,B为入射点, 若出射光线CD与MN的交点P到球心O的距离是球半径的 倍,且与MN所成的角α=30°,求:此透明体折射率和单色光在透明球体中的波长。
倍,且与MN所成的角α=30°,求:此透明体折射率和单色光在透明球体中的波长。
282nm
解析试题分析:连接OB 、BC,如图D-2。 在B点光线的入射角、折射角分别标为i、r,
在 OCP中:有
OCP中:有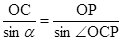 解得:
解得: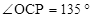 (45°值舍)
(45°值舍)
进而可得: 2分
2分
由折射率定义: 在B点有: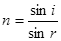
在C点有: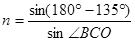
又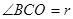 所以,i=45° 2分
所以,i=45° 2分
又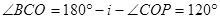 故r=30° 1分
故r=30° 1分
因此,透明体的折射率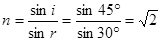 2分
2分
(2)因为: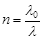 ,所以单色光在透明体中的波长
,所以单色光在透明体中的波长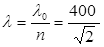 nm="282nm" 2分
nm="282nm" 2分
考点:本题考查光的折射、正弦定理和几何关系。

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
某同学用某种单色光做杨氏双缝干涉实验时,发现条纹太密难以测量,可以采用的改善办法是
| A.增大双缝间距 |
| B.增大双缝到屏的距离 |
| C.增大双缝到单缝的距离 |
| D.改用波长较长的光(如红光)作为入射光 |
 的玻璃制成的三棱镜截面。平行光线由AB面入射,从BC面射出时光线与BC面垂直。则斜射到AB面上光线的入射角是多少?斜射到AB面上的光束,并能从BC面上射出的那部分光束宽度是AB边长的多少倍?
的玻璃制成的三棱镜截面。平行光线由AB面入射,从BC面射出时光线与BC面垂直。则斜射到AB面上光线的入射角是多少?斜射到AB面上的光束,并能从BC面上射出的那部分光束宽度是AB边长的多少倍?

 。这两条光线射出玻璃砖后相交于一点,该点到O点的距离为
。这两条光线射出玻璃砖后相交于一点,该点到O点的距离为 ,求玻璃砖的折射率。
,求玻璃砖的折射率。
 ,直径AB与屏幕MN垂直并接触于A点。激光a以入射角i=60°射向玻璃砖圆心O,结果在屏幕MN上出现两光斑,求两光斑之间的距离L。
,直径AB与屏幕MN垂直并接触于A点。激光a以入射角i=60°射向玻璃砖圆心O,结果在屏幕MN上出现两光斑,求两光斑之间的距离L。

 ,0≤α≤
,0≤α≤ ,求β的最小值.
,求β的最小值. ,半径为R、长为L.一平行光束从半圆柱体的矩形表面垂直射入,从部分柱面有光线射出.求该部分柱面的面积S.
,半径为R、长为L.一平行光束从半圆柱体的矩形表面垂直射入,从部分柱面有光线射出.求该部分柱面的面积S.
 ,此单色光通过玻璃体后沿BD方向射出,且与x轴交于D点,OD=
,此单色光通过玻璃体后沿BD方向射出,且与x轴交于D点,OD= ,求:
,求: