Question

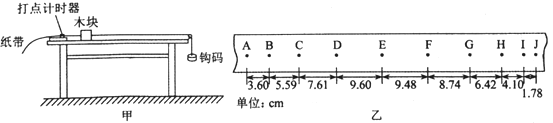
【题目】如图所示，倾角为θ=37°的足够长平行光滑的两导轨，间距为L=1 m，导轨间有垂直于轨道平面向下的磁场，磁感应强度大小B1=1T；底端ab间连一电阻R1=3Ω；顶端通过导线连接一横截面积为S=0.1m2、总电阻为r=0.8Ω、匝数N=100匝的线圈（线圈中轴线沿竖直方向），线圈内有沿竖直方向、且随时间均匀变化的磁场B2。一质量为m=0.1kg、电阻为R2=2Ω、长度也为L的导体棒cd横放在导轨上，导体棒与导轨始终良好接触。不计导轨和导线的电阻，取g=10m/s2, sin37°=0.6，求：

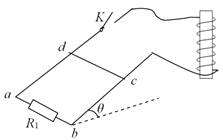
（1）若断开开关K，静止释放导体棒，则导体棒能达到的最大速率是多少？此时cd两端电势差Ucd为多少？

（2）若闭合开关K，为使导体棒始终静止在导轨上，判断线圈中所加磁场的方向并计算其变化率的大小。

Answer 1

【答案】（1）3m/s；1.8V（2）线圈中所加磁场如果在增强，方向为竖直向下；如果在减弱，方向为竖直向上。0.2T/s

【解析】

（1）当导体棒达到最大速度时，安培力等于重力沿斜面向下的分力，列式求解最大速度；（2）根据法拉第电磁感应定律求解；根据楞次定律判断磁场的方向。

（1）当导体棒达到最大速度时，F安= B1IL =mgsin37°

由,

E=B1Lv

得v=3m/s

Ucd=IR1=1.8V

（2）线圈中的感应电动势 =I总R总

其中I总==1A

R总=R并+r=2Ω

得=0.2T/s

由楞次定律可知，线圈中所加磁场如果在增强，方向为竖直向下；如果在减弱，方向为竖直向上。