题目内容
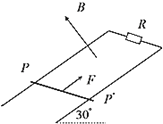
【题目】如图所示，间距L=1m的足够长的光滑平行金属导轨与水平面成30°角放置，导轨电阻不计，导轨上端连有R=0.8Ω的电阻，磁感应强度为B=1T的匀强磁场垂直导轨平面向上，t=0时刻有一质量m=1kg，电阻r=0.2Ω的金属棒，以v0=10m/s的初速度从导轨上某一位置PP'开始沿导轨向上滑行，金属棒垂直导轨且与导轨接触良好，与此同时对金属棒施加一个沿斜面向上且垂直于金属棒的外力F，使金属棒做加速度大小为2m/s2的匀减速直线运动，则：
（1）t=2s时，外力F的大小？
（2）若已知金属棒运动从开始运动到最高点的过程中，回路中产生的热量为166.7J，求此过程中外力F做的功？
（3）到最高点后，撤去外力F，经过足够长时间后，最终电阻R上消耗的热功率是多少？
【答案】（1）F =9N （2）
（3）
【解析】
（1）根据运动学公式求解t=2s时的速度，然后根据切割公式求解感应电动势，根据闭合电路欧姆定律求解感应电流，根据安培力公式求解安培力，最后受力分析，根据牛顿第二定律求解拉力；
（2）对上升过程，先根据运动学公式求解位移，再根据功能关系列式求解；
（3）到最高点后，撤去外力F，经过足够长时间后，金属棒匀速下降，根据平衡条件求解最大速度，再根据P=Fv求解克服安培力做功的功率，最后根据功率分配关系求解电阻R上消耗的热功率．
（1）金属棒匀减速上升，根据速度时关系公式，有
v1=v0-at=10-2×2=6m/s
解得：F =9N
（2）根据速度位移关系公式，到最高点的位移：
由动能定理，得： 
解得：
（3）如图所示，最后稳定时导体棒的速度满足：
根据功率分配关系，有：
解得： PR=20W
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
