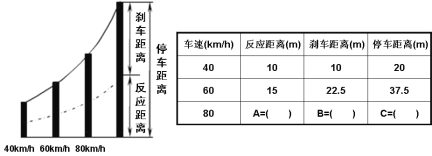
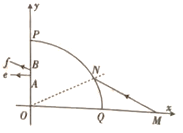
题目内容
【题目】某兴趣小组举行遥控赛车比赛,比赛轨道如图所示:水平直线轨道与光滑竖直半圆轨道BC相切与B点。一辆可视为质点的赛车从起点A出发,沿水平直线轨道向右运动,由B点进入光滑竖直半圆轨道,并通过轨道的最高点C作平抛运动,落地后才算完成比赛。已知光滑竖直半圆轨道半径为R = O.4m、赛车质量m = O.5 kg。通电后赛车电动机以额定功率P =4W工作,赛车在水平轨道上受到的阻力恒为f = O.4 N, g取1Om/s2 。则:
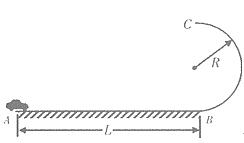
(1)若 AB间距离L=10m,要使赛车能完成比赛,电动机至少要工作多长时间?
(2)若赛车在B点速度vB= 8.Om/s,问半圆轨道半径R改变为多少时赛车能完成比赛,且落地点离B点最远?
【答案】(1)2.25s(2)0.8m
【解析】
(1)赛车刚好能过C点时,赛车仅由重力提供向心力,即 mg=![]()
设电动机工作最短时间为t1,赛车由A点到C点的过程中,由动能定理W总=Δk ,得:
Pt1- fL-2 mg R =![]() - 0
- 0
得t1=2.25s
(2)设赛车过C点速度为vC,B点所在水平面为零势能参考平面,赛车由B点运动到C点的过程中,由机械能守恒定律得:![]() +0=
+0=![]() +2mgR
+2mgR
赛车过C点后平抛:2R= ![]() gt22
gt22
x=vC t2
整理上式得 ![]()
由数学知识得![]() 时,平抛的水平距离x最大,即
时,平抛的水平距离x最大,即![]() =0.8m
=0.8m

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目