题目内容
飞船竖直降落过程中,在离地面高度h处的速度为V0,此时开动反冲火箭,使飞船开始做减速运动,最后着地时的速度V.若把这一过程当作匀减速运动来计算,已知地球表面附近的重力加速度为g,航天员的质量m.求:
(1)上述过程中航天员运动的加速度大小.
(2)上述过程中航天员对坐椅的压力.
(1)上述过程中航天员运动的加速度大小.
(2)上述过程中航天员对坐椅的压力.
分析:(1)根据匀变速直线运动的速度位移公式求出航天员的加速度大小.
(2)抓住宇航员与飞船具有相同的加速度,根据牛顿第二定律求出支持力的大小,从而根据牛顿第三定律求出 航天员对座椅的压力.
(2)抓住宇航员与飞船具有相同的加速度,根据牛顿第二定律求出支持力的大小,从而根据牛顿第三定律求出 航天员对座椅的压力.
解答:解:(1)匀变速运动规律可知:
V02-V2=2ah,
解得:a=
.
(2)牛顿第二定律得:
mg-N=ma.
所以有:N=m(g-a)=m[g-
]
根据牛顿第三定律,宇航员对坐椅的压力:N′=N=m[g-
].
答:(1)上述过程中航天员运动的加速度大小a=
.
(2)上述过程中航天员对坐椅的压力为m[g-
].
V02-V2=2ah,
解得:a=
| V02-V2 |
| 2h |
(2)牛顿第二定律得:
mg-N=ma.
所以有:N=m(g-a)=m[g-
| V22-V2 |
| 2h |
根据牛顿第三定律,宇航员对坐椅的压力:N′=N=m[g-
| V22-V2 |
| 2h |
答:(1)上述过程中航天员运动的加速度大小a=
| V02-V2 |
| 2h |
(2)上述过程中航天员对坐椅的压力为m[g-
| V22-V2 |
| 2h |
点评:本题考查了运动学公式和牛顿第二定律的基本运用,知道加速度是联系力学和运动学的桥梁.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 “神舟七号”飞船完成了预定空间科学和技术实验任务后,返回舱于2008年9月28日17时37分开始从太空向地球表面按预定轨道返回,在离地10km 的高度打开阻力降落伞减速下降,这一过程中若返回舱所受阻力与速度的平方成正比,比例系数(空气阻力系数)为k.设返回舱总质量M=3000kg,所受空气浮力恒定不变,且认为竖直降落.从某时刻开始计时.返回舱的运动v--t图象如图中的AD曲线所示,图中AB是曲线在A点的切线,切线交于横轴一点B的坐标为(8,0),CD是平行横轴的直线,交纵轴于C点,c的坐标为(0,8).g取10m/s2,请回答下列问题:
“神舟七号”飞船完成了预定空间科学和技术实验任务后,返回舱于2008年9月28日17时37分开始从太空向地球表面按预定轨道返回,在离地10km 的高度打开阻力降落伞减速下降,这一过程中若返回舱所受阻力与速度的平方成正比,比例系数(空气阻力系数)为k.设返回舱总质量M=3000kg,所受空气浮力恒定不变,且认为竖直降落.从某时刻开始计时.返回舱的运动v--t图象如图中的AD曲线所示,图中AB是曲线在A点的切线,切线交于横轴一点B的坐标为(8,0),CD是平行横轴的直线,交纵轴于C点,c的坐标为(0,8).g取10m/s2,请回答下列问题: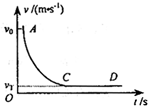 飞船完成了在顶定空间的科学技术试验后,返回舱开始按预定轨道从太空向地球表面返回.返回舱开始时通过自身发动机进行调控以减速下降,进入大气层后,在一定的高度关闭发动机,打开阻力降落伞进一步减速下降.这一过程中,返回舱所受空气摩擦阻力与其速度的平方成正比,比例系数(空气阻力系数)为k.若返回舱所受空气浮力忽略不计,且认为竖直降落,从阻力伞打开开始计时,返回舱运动的v-t图象如图中的AD曲线所示(其中CD段是平行横坐标轴的直线),已知返回舱的总质量为m,重力加速度g,求:
飞船完成了在顶定空间的科学技术试验后,返回舱开始按预定轨道从太空向地球表面返回.返回舱开始时通过自身发动机进行调控以减速下降,进入大气层后,在一定的高度关闭发动机,打开阻力降落伞进一步减速下降.这一过程中,返回舱所受空气摩擦阻力与其速度的平方成正比,比例系数(空气阻力系数)为k.若返回舱所受空气浮力忽略不计,且认为竖直降落,从阻力伞打开开始计时,返回舱运动的v-t图象如图中的AD曲线所示(其中CD段是平行横坐标轴的直线),已知返回舱的总质量为m,重力加速度g,求: