题目内容
1. 距地面高5m的水平直轨道上A、B两点相距2m,在B点用细线悬挂一小球,离地高度为h,如图.小车始终以4m/s的速度沿轨道匀速运动,经过A点时将随车携带的小球由轨道高度自由卸下,小车运动至B点时细线被轧断,最后两球同时落地.不计空气阻力,取重力加速度的大小g=10m/s2.可求得h等于( )
距地面高5m的水平直轨道上A、B两点相距2m,在B点用细线悬挂一小球,离地高度为h,如图.小车始终以4m/s的速度沿轨道匀速运动,经过A点时将随车携带的小球由轨道高度自由卸下,小车运动至B点时细线被轧断,最后两球同时落地.不计空气阻力,取重力加速度的大小g=10m/s2.可求得h等于( )| A. | 1.25m | B. | 2.25m | C. | 3.75m | D. | 4.75m |
分析 经过A点时将随车携带的小球由轨道高度自由卸下后,小球做平抛运动,小车运动至B点时细线被轧断,则B处的小球做自由落体运动,根据平抛运动及自由落体运动基本公式抓住时间关系列式求解.
解答 解:经过A点,将球自由卸下后,A球做平抛运动,则有:
H=$\frac{1}{2}g{{t}_{1}}^{2}$
解得:${t}_{1}=\sqrt{\frac{2×5}{10}}=1s$,
小车从A点运动到B点的时间${t}_{2}=\frac{{x}_{AB}}{v}=\frac{2}{4}=0.5s$,
因为两球同时落地,则细线被轧断后B处小球做自由落体运动的时间为t3=t1-t2=1-0.5=0.5s,
则h=$\frac{1}{2}g{t}^{2}=\frac{1}{2}×10×0.{5}^{2}=1.25m$
故选:A
点评 本题主要考查了平抛运动和自由落体运动基本公式的直接应用,关键抓住同时落地求出B处小球做自由落体运动的时间,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 某同学利用如图所示装置测量弹簧的劲度系数,弹簧上端固定在铁架台上,下端装有指针及挂钩,指针恰好指向一把竖直立起的毫米刻度尺的刻度.
某同学利用如图所示装置测量弹簧的劲度系数,弹簧上端固定在铁架台上,下端装有指针及挂钩,指针恰好指向一把竖直立起的毫米刻度尺的刻度.
(1)在挂钩上分别挂上不同数量的钩码,并相应记录指针在刻度尺上所指的刻度值,填入下表:
由表格可知,每增加一个钩码,弹簧形变量的平均值为1.56cm(结果保留三位有效数字)
(2)已知每个钩码的质量为m0=50g,当地重力加速度g=9.8m/s2.求弹簧的劲度系数=32N/m;
(3)考虑到在没有挂钩码时弹簧自身有重量,测量的劲度系数与真实值相比较没有影响(填偏大、偏小、没有影响)
 某同学利用如图所示装置测量弹簧的劲度系数,弹簧上端固定在铁架台上,下端装有指针及挂钩,指针恰好指向一把竖直立起的毫米刻度尺的刻度.
某同学利用如图所示装置测量弹簧的劲度系数,弹簧上端固定在铁架台上,下端装有指针及挂钩,指针恰好指向一把竖直立起的毫米刻度尺的刻度.(1)在挂钩上分别挂上不同数量的钩码,并相应记录指针在刻度尺上所指的刻度值,填入下表:
| 钩码数n | 0 | 1 | 2 | 3 | 4 | 5 |
| 刻度尺读数xn(cm) | 2.62 | 4.17 | 5.70 | 7.22 | 8.84 | 10.43 |
(2)已知每个钩码的质量为m0=50g,当地重力加速度g=9.8m/s2.求弹簧的劲度系数=32N/m;
(3)考虑到在没有挂钩码时弹簧自身有重量,测量的劲度系数与真实值相比较没有影响(填偏大、偏小、没有影响)
16.科学家使用核反应获取氚,再利用氘和氚的核反应获得能量,核反应方程分别为:X+Y→${\;}_{2}^{4}$He+${\;}_{1}^{3}$H+4.9MeV和${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+X+17.6MeV.下列表述正确的有( )
| A. | X是中子 | B. | Y的质子数是3,中子数是6 | ||
| C. | 两个核反应都没有质量亏损 | D. | 氘和氚的核反应是核聚变反应 |
13.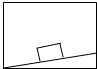 如图,升降机内有一固定斜面,斜面上放一物块.开始时,升降机做匀速运动,物块相对于斜面匀速下滑.当升降机加速上升时,( )
如图,升降机内有一固定斜面,斜面上放一物块.开始时,升降机做匀速运动,物块相对于斜面匀速下滑.当升降机加速上升时,( )
 如图,升降机内有一固定斜面,斜面上放一物块.开始时,升降机做匀速运动,物块相对于斜面匀速下滑.当升降机加速上升时,( )
如图,升降机内有一固定斜面,斜面上放一物块.开始时,升降机做匀速运动,物块相对于斜面匀速下滑.当升降机加速上升时,( )| A. | 物块与斜面间的摩擦力减少 | B. | 物块与斜面间的正压力增大 | ||
| C. | 物块相对于斜面减速下滑 | D. | 物块相对于斜面匀速下滑 |
10.对动能定理的理解正确的是( )
| A. | 外力做功是引起物体动能变化的原因 | |
| B. | 动能的变化使物体产生了功 | |
| C. | 外力做的功变成了物体的动能 | |
| D. | 外力对物体做了多少功,物体的动能就改变多少 |
 如图所示,在虚线MN的右侧存在着垂直纸面向里的匀强磁场,边长为a的正三角形金属线框平行纸面放置,t=0时刻,顶点恰好在磁场的左边界上,一边平行磁场边界MN,现令该金属线框匀速进入磁场区域,则线框中产生的感应电动势E,电流I、所施加的外力F、安培力做功的功率P随机t的变化关系的图象中正确的是( )
如图所示,在虚线MN的右侧存在着垂直纸面向里的匀强磁场,边长为a的正三角形金属线框平行纸面放置,t=0时刻,顶点恰好在磁场的左边界上,一边平行磁场边界MN,现令该金属线框匀速进入磁场区域,则线框中产生的感应电动势E,电流I、所施加的外力F、安培力做功的功率P随机t的变化关系的图象中正确的是( )

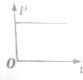
 某同学在“探究弹力和弹簧伸长的关系”时,安装好实验装置,让刻度尺零刻度与弹簧上端平齐,在弹簧下端挂1个钩码,静止时弹簧长度为l1,如图1所示,图2是此时固定在弹簧挂钩上的指针在刻度尺(最小分度是1毫米)上位置的放大图,示数l1=25.85cm.在弹簧下端分别挂2个、3个、4个、5个相同钩码,静止时弹簧长度分别是l2、l3、l4、l5,已知每个钩码质量是50g,挂2个钩码时,弹簧弹力F2=0.98N(当地重力加速度g=9.8m/s2).要得到弹簧伸长量x,还需要测量的是弹簧原长.作出F-x曲线,得到弹力与弹簧伸长量的关系.
某同学在“探究弹力和弹簧伸长的关系”时,安装好实验装置,让刻度尺零刻度与弹簧上端平齐,在弹簧下端挂1个钩码,静止时弹簧长度为l1,如图1所示,图2是此时固定在弹簧挂钩上的指针在刻度尺(最小分度是1毫米)上位置的放大图,示数l1=25.85cm.在弹簧下端分别挂2个、3个、4个、5个相同钩码,静止时弹簧长度分别是l2、l3、l4、l5,已知每个钩码质量是50g,挂2个钩码时,弹簧弹力F2=0.98N(当地重力加速度g=9.8m/s2).要得到弹簧伸长量x,还需要测量的是弹簧原长.作出F-x曲线,得到弹力与弹簧伸长量的关系. 如图所示,直径分别为D和2D的同心圆处于同一竖直面内,O为圆心,GH为大圆的水平直径.两圆之间的环形区域(Ⅰ区)和小圆内部(Ⅱ区)均存在垂直圆面向里的匀强磁场.间距为d的两平行金属极板间有一匀强电场,上级板开有一小孔.一质量为m,电量为+q的粒子由小孔下方$\frac{d}{2}$处静止释放,加速后粒子以竖直向上的速度v射出电场,由H点紧靠大圆内侧射入磁场.不计粒子的重力.
如图所示,直径分别为D和2D的同心圆处于同一竖直面内,O为圆心,GH为大圆的水平直径.两圆之间的环形区域(Ⅰ区)和小圆内部(Ⅱ区)均存在垂直圆面向里的匀强磁场.间距为d的两平行金属极板间有一匀强电场,上级板开有一小孔.一质量为m,电量为+q的粒子由小孔下方$\frac{d}{2}$处静止释放,加速后粒子以竖直向上的速度v射出电场,由H点紧靠大圆内侧射入磁场.不计粒子的重力.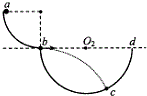 如图所示,半径为r1=1.8m的$\frac{1}{4}$光滑圆弧轨道末端水平,固定在水平地面上,与竖直截面为半圆形的坑平滑连接,bd为坑沿水平方向的直径.现将质量为m=1.0kg的小球从圆弧顶端a点由静止释放,小球离开b点后击中坑壁上的c点.测得c点与水平地面的竖直距离为h=1.8m,重力加速度g取10m/s2.求:
如图所示,半径为r1=1.8m的$\frac{1}{4}$光滑圆弧轨道末端水平,固定在水平地面上,与竖直截面为半圆形的坑平滑连接,bd为坑沿水平方向的直径.现将质量为m=1.0kg的小球从圆弧顶端a点由静止释放,小球离开b点后击中坑壁上的c点.测得c点与水平地面的竖直距离为h=1.8m,重力加速度g取10m/s2.求: