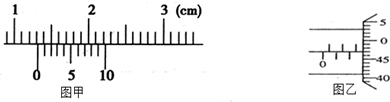
题目内容
5.当人造地球卫星的轨道半径变为原来的3倍,则( )| A. | 由v=ωr得线速度也变为原来的3倍 | |
| B. | 由ω=$\frac{v}{r}$得角速度变为原来的$\frac{1}{3}$ | |
| C. | 由a=$\frac{{v}^{2}}{r}$得向心加速度变为原来的$\frac{1}{3}$ | |
| D. | 由$\frac{{r}^{3}}{{T}^{2}}$=K得周期变为原来的$\sqrt{27}$倍 |
分析 根据万有引力提供圆周运动向心力由轨道半径变化关系分析其它物理量的变化,注意控制变量法的应用.
解答 解:根据万有引力提供圆周运动向心力有$G\frac{mM}{{r}^{2}}=mr{ω}^{2}=m\frac{{v}^{2}}{r}=mr\frac{4{π}^{2}}{{T}^{2}}$有:
A、卫星的角速度$ω=\sqrt{\frac{GM}{{r}^{3}}}$随半径变化,故据v=ωr不能得出线速度与半径成正比,故A错误;
B、卫星的线速度$v=\sqrt{\frac{GM}{r}}$随半径变化,故不能根据$ω=\frac{v}{r}$得出角速度与半径成反比的结论,故B错误;
C、卫星的线速度$v=\sqrt{\frac{GM}{r}}$随半径变化,故不能据a=$\frac{{v}^{2}}{r}$得出加速度与半径成反比的结论,故C错误;
D、根据开普勒行星运动定律$\frac{{r}^{3}}{{T}^{2}}=K$,可知当半径r变为原来的3倍时,周期变为原来的$\sqrt{27}$倍,故D正确.
故选:D.
点评 能根据万有引力提供圆周运动向心力分析轨道半径变化引起其它描述圆周运动物理量的变化,根据表达式确定物理量关系时要注意其它变量的控制.

练习册系列答案
相关题目
13. 如图所示.将一阴极射线管置于一通电螺线管的正上方h且在同一水平面内,从射线管的阴极不断有电子射向阳极,则阴极射线将( )
如图所示.将一阴极射线管置于一通电螺线管的正上方h且在同一水平面内,从射线管的阴极不断有电子射向阳极,则阴极射线将( )
 如图所示.将一阴极射线管置于一通电螺线管的正上方h且在同一水平面内,从射线管的阴极不断有电子射向阳极,则阴极射线将( )
如图所示.将一阴极射线管置于一通电螺线管的正上方h且在同一水平面内,从射线管的阴极不断有电子射向阳极,则阴极射线将( )| A. | 向纸外偏转 | B. | 向纸内偏转 | C. | 向上偏转 | D. | 向下偏转 |
20. 如图,穿在足够长的水平直杆上质量为m的小球开始时静止.现对小球沿杆方向施加恒力F0,垂直于杆方向施加竖直向上的力F,且F的大小始终与小球的速度成正比,即F=kv(图中未标出).已知小球与杆间的动摩擦因数为μ,且F0>μmg.下列说法正确的是( )
如图,穿在足够长的水平直杆上质量为m的小球开始时静止.现对小球沿杆方向施加恒力F0,垂直于杆方向施加竖直向上的力F,且F的大小始终与小球的速度成正比,即F=kv(图中未标出).已知小球与杆间的动摩擦因数为μ,且F0>μmg.下列说法正确的是( )
 如图,穿在足够长的水平直杆上质量为m的小球开始时静止.现对小球沿杆方向施加恒力F0,垂直于杆方向施加竖直向上的力F,且F的大小始终与小球的速度成正比,即F=kv(图中未标出).已知小球与杆间的动摩擦因数为μ,且F0>μmg.下列说法正确的是( )
如图,穿在足够长的水平直杆上质量为m的小球开始时静止.现对小球沿杆方向施加恒力F0,垂直于杆方向施加竖直向上的力F,且F的大小始终与小球的速度成正比,即F=kv(图中未标出).已知小球与杆间的动摩擦因数为μ,且F0>μmg.下列说法正确的是( )| A. | 小球先做加速度减小的加速运动,后做加速度增大的减速运动直到静止 | |
| B. | 小球先做加速度增大的加速运动,后做加速度减小的加速运动,直到最后做匀速运动 | |
| C. | 小球的最大加速度为$\frac{{F}_{0}}{m}$ | |
| D. | 恒力F0的最大速度为$\frac{{F}_{0}}{μk}$+$\frac{mg}{k}$ |
10. 如图所示是一实验电路图,电动势为E、内阻为r的电池与定值电阻R0、滑动变阻器R串联,已知R0=r,滑动变阻器的最大阻值是2r.当滑动变阻器的滑片P由a端向b端滑动时,下列说法中正确的是( )
如图所示是一实验电路图,电动势为E、内阻为r的电池与定值电阻R0、滑动变阻器R串联,已知R0=r,滑动变阻器的最大阻值是2r.当滑动变阻器的滑片P由a端向b端滑动时,下列说法中正确的是( )
 如图所示是一实验电路图,电动势为E、内阻为r的电池与定值电阻R0、滑动变阻器R串联,已知R0=r,滑动变阻器的最大阻值是2r.当滑动变阻器的滑片P由a端向b端滑动时,下列说法中正确的是( )
如图所示是一实验电路图,电动势为E、内阻为r的电池与定值电阻R0、滑动变阻器R串联,已知R0=r,滑动变阻器的最大阻值是2r.当滑动变阻器的滑片P由a端向b端滑动时,下列说法中正确的是( )| A. | 电流表的示数变小,电压表示数变大 | |
| B. | 定值电阻R0上消耗的功率变小 | |
| C. | 滑动变阻器消耗的功率变小 | |
| D. | 电源的效率增大 |
14.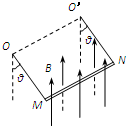 如图所示,质量为m、长度为L的金属棒MN两端由等长的轻质细线水平悬挂在O、O′点,处于竖直向上的匀强磁场中,磁感应强度大小为B;棒中通以某一方向的电流,平衡时两悬线与竖直方向夹角均为θ,重力加速度为g,则( )
如图所示,质量为m、长度为L的金属棒MN两端由等长的轻质细线水平悬挂在O、O′点,处于竖直向上的匀强磁场中,磁感应强度大小为B;棒中通以某一方向的电流,平衡时两悬线与竖直方向夹角均为θ,重力加速度为g,则( )
 如图所示,质量为m、长度为L的金属棒MN两端由等长的轻质细线水平悬挂在O、O′点,处于竖直向上的匀强磁场中,磁感应强度大小为B;棒中通以某一方向的电流,平衡时两悬线与竖直方向夹角均为θ,重力加速度为g,则( )
如图所示,质量为m、长度为L的金属棒MN两端由等长的轻质细线水平悬挂在O、O′点,处于竖直向上的匀强磁场中,磁感应强度大小为B;棒中通以某一方向的电流,平衡时两悬线与竖直方向夹角均为θ,重力加速度为g,则( )| A. | 金属棒中的电流方向由N指向M | |
| B. | 金属棒MN所受安培力的方向垂直于OMNO′平面向上 | |
| C. | 金属棒中的电流大小为$\frac{mg}{BL}$tanθ | |
| D. | 每条悬线所受拉力大小为mgcosθ |
13.关于电场强度的叙述,正确的是( )
| A. | 沿着电场线的方向,场强越来越小 | |
| B. | 电场中某点的场强大小等于单位电量的电荷在该点所受的电场力大小 | |
| C. | 电势降落的方向就是场强的方向 | |
| D. | 负点电荷形成的电场,离点电荷越近,场强越小 |
 如图所示,xOy坐标系内有匀强磁场,磁感应强度为B,方向垂直纸面向里,x<0的区域内有匀强电场(图中未画出).x>0区域有一半径为R的圆柱形圆筒,圆心O1的坐标为(2R,0),圆筒轴线与磁场平行,现有范围足够大的平行电子束恰能沿x轴正方向做匀速直线通过x<0区域,已知电子的质量为m、电荷量为e,不考虑电子间的相互作用,不计电子重力.求:
如图所示,xOy坐标系内有匀强磁场,磁感应强度为B,方向垂直纸面向里,x<0的区域内有匀强电场(图中未画出).x>0区域有一半径为R的圆柱形圆筒,圆心O1的坐标为(2R,0),圆筒轴线与磁场平行,现有范围足够大的平行电子束恰能沿x轴正方向做匀速直线通过x<0区域,已知电子的质量为m、电荷量为e,不考虑电子间的相互作用,不计电子重力.求: