题目内容
【题目】如图所示,四个半径为1,且完全相同的均质光滑圆球,将它们摆为上下两层且彼此相切,下层三个球![]() 、
、![]() 、
、![]() 质量均为
质量均为![]() ,放置在光滑水平面上,上层球
,放置在光滑水平面上,上层球![]() 的质量为下边三个球质量之和.试
的质量为下边三个球质量之和.试
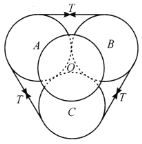
(1)若将下层三个球用一根绳子在球心高度处缠绕,把三个球捆扎在一起,再将第四个球放在上层,问:静止情况下张力![]() 为多大?
为多大?
(2)若在图所示的位置突然剪断绳子,四个球由静止开始运动,问:上下层球在什么位置处开始脱离?
(3)问:上层球第一次落到桌面时,下层三个球的质心运动后所组成等边三角形的边长为多大?
【答案】(1)![]() (2)
(2)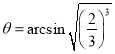 时上下层球开始脱离(3)
时上下层球开始脱离(3)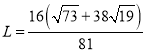
【解析】
设下层球的质量均为![]() ,则上层球的质量为
,则上层球的质量为![]() .
.![]() 、
、![]() 、
、![]() 、
、![]() 分别为下层球和上层球的球心,
分别为下层球和上层球的球心,![]() 为下层球心组成三角形的形心,
为下层球心组成三角形的形心,![]() 为
为![]() 与
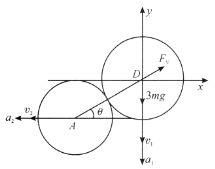
与![]() 的夹角,如图所示.
的夹角,如图所示.

(1)系统静止时,由几何关系可知![]() ,
,![]() .
.
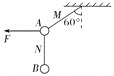
对上层球![]() 进行受力分析,如图所示,列
进行受力分析,如图所示,列![]() 方向平衡方程有
方向平衡方程有
![]() ,
,![]() . ①
. ①
图3
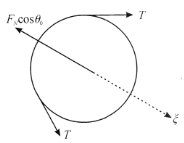
对下层球![]() 进行受力分析,如图所示,列
进行受力分析,如图所示,列![]() 方向平衡方程有
方向平衡方程有
![]() ,
,![]() . ②
. ②
联立式①②,可得系统静止时绳子拉力为![]() .
.
(2)开始时上下层球心的连线与水平方向夹角为![]() ,剪断绳子后在
,剪断绳子后在![]() 位置,设下层球心水平速度为
位置,设下层球心水平速度为![]() ,加速度为
,加速度为![]() ,上层球球心下落的速度为
,上层球球心下落的速度为![]() ,加速度为
,加速度为![]() .
.
两球脱离前![]() .
.
由系统的动能定理,有![]() .
.
整理可得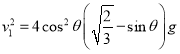 , ③
, ③
由刚体运动学原理,上下层球脱离前,下层任一球与上层球球心的加速度之间有如下关系:
![]() . ④
. ④
设上层球与下层三球间的相互作用力为![]() ,对上层球分析,由质心运动定理有
,对上层球分析,由质心运动定理有
![]() . ⑤
. ⑤
对下层任一球进行分析,由质心运动定理有
![]() . ⑥
. ⑥
由式③⑥,可得上下层球相互作用力为
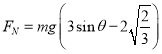 . ⑦
. ⑦
上下层球脱离条件为![]() ,由式⑦得
,由式⑦得![]() .
.
即当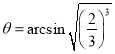 时上下层球开始脱离
时上下层球开始脱离
(3)上下层球脱离后,上层与下层球球心的距离始终大于2,上下两层球不再相碰,将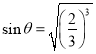 代人式③,可以求出脱离时上层球心的速度为
代人式③,可以求出脱离时上层球心的速度为
![]() . ⑧
. ⑧
此时,下层球的质心速度为
![]() . ⑨
. ⑨
运动后,下层球心到静正时下层球心围成的等边三角形中心的距离为
![]() . ⑩
. ⑩
上层球心到桌面间的距离为
![]() .
.
由式⑧,脱离后上层球接触桌面所需的时间为
 .
.
由式⑨,下层球心在这段时间内又运动距离为
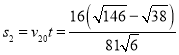 .
.
由式⑩,当上层球第一次与桌面接触时,下层三个球的质心所组成的等边三角形的边长是
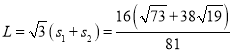

 阅读快车系列答案
阅读快车系列答案