题目内容
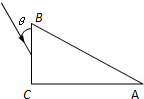 (2010?德州一模)如图所示,一个截面为直角三角形的三棱镜,∠A=30°,∠C=90°.三棱镜材料的折射率n=
(2010?德州一模)如图所示,一个截面为直角三角形的三棱镜,∠A=30°,∠C=90°.三棱镜材料的折射率n=| 3 |
①求光在三棱镜中的传播速度;
②求从AB边射出光线与AB边的夹角.
分析:根据v=
求出光在三棱镜中的传播速度.求出光在介质中发生全反射的临界角,结合几何关系,运用折射定律求出从AB边射出光线与AB边的夹角.
| c |
| n |
解答:解:(1)光在三棱镜中的传播速度v=
=
=1.73×108m/s.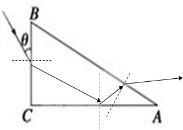
(2)根据折射定律得,
=n,解得光在BC面上折射角为30°.根据几何关系得,光在AC面上的入射角为60°.
因为sinC=
=
,因为sin60°>sinC,所以光在AC面上发生全反射,根据几何关系知光在AB面上的入射角为30°
根据
=n,解得β=60°,则光从AB边的出射光线与AB边的夹角为30°.
答:(1)光在三棱镜中的传播速度为1.73×108m/s.
(2)从AB边射出光线与AB边的夹角为30°.
| c |
| n |
| 3×108 | ||
|

(2)根据折射定律得,
| sin(90°-θ) |
| sinα |
因为sinC=
| 1 |
| n |
| ||
| 3 |
根据
| sinβ |
| sin30° |
答:(1)光在三棱镜中的传播速度为1.73×108m/s.
(2)从AB边射出光线与AB边的夹角为30°.
点评:解决本题的关键是滑出光路图,运用折射定律和几何关系进行求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2010?德州一模)如图所示,真空中有两个等量异种点电荷A、B,M、N、O是AB连线的垂线上的点,且AO>OB.一带负电的试探电荷仅受电场力作用,运动轨迹如图中实线所示,设M、N两点的场强大小分别EM、EN,电势分别为φM、φN.下列判断中正确的是( )
(2010?德州一模)如图所示,真空中有两个等量异种点电荷A、B,M、N、O是AB连线的垂线上的点,且AO>OB.一带负电的试探电荷仅受电场力作用,运动轨迹如图中实线所示,设M、N两点的场强大小分别EM、EN,电势分别为φM、φN.下列判断中正确的是( )
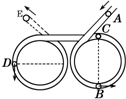 (2010?德州一模)2009年是中华人民共和国成立60周年,南莫中学物理兴趣小组用空心透明塑料管制作了如图所示的竖直“60”造型.两个“0”字型的半径均为R.让一质量为m、直径略小于管径的光滑小球从入口A处射入,依次经过图中的B、C、D三点,最后从E点飞出.已知BC是“0”字型的一条直径,D点是该造型最左侧的一点,当地的重力加速度为g,不计一切阻力,则小球在整个运动过程中( )
(2010?德州一模)2009年是中华人民共和国成立60周年,南莫中学物理兴趣小组用空心透明塑料管制作了如图所示的竖直“60”造型.两个“0”字型的半径均为R.让一质量为m、直径略小于管径的光滑小球从入口A处射入,依次经过图中的B、C、D三点,最后从E点飞出.已知BC是“0”字型的一条直径,D点是该造型最左侧的一点,当地的重力加速度为g,不计一切阻力,则小球在整个运动过程中( )