Question

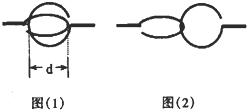
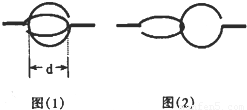
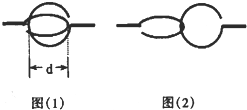列车载重时直接向前起动有困难，司机常常先倒车再起动前进．设在平直轨道上的某机车后面挂接有n节车厢，机车与每节车厢的质量都为m，它们所受的阻力都为自身重力的k倍，倒车后各节车厢间的挂钩所留间隙均为d，如图（1）所示，在这种植况下，机车以恒定的牵引力F由静止开始起动，机车及各车厢间挂接的时间极短，挂接后挂钩的状态如图（2）所示．求：
（1）第一节车厢刚被带动时列车的速度
（2）最后一节车厢刚被带动时列车的速度
（3）要想使最后一节车厢也能被带动起来，机车牵引力 F的最小值．

Answer 1

分析：（1）由动能定理可以求出挂接第一节车厢时机车的速度，挂接车厢时机车与车厢组成的系统动量守恒，由动量守恒定律可以求出列车的速度．
（2）由动能定理与动量守恒定律可以求出最后一节车厢刚被带动时列车的速度．
（3）最后一节车厢被带动起来的条件是，列车的速度大于等于零，据此求出拉力大小．

解答：解：（1）挂接第一节车厢前，由动能定理得：
（F-kmg）d=

1

2

mv₁′²-0，
挂接第一节车厢的过程中，动量守恒，
由动量守恒定律得：mv₁′=2mv₁，
解得：v₁=

1 2 ( F m -kg)d

；
（2）挂接第二节车厢前，由动能定理得：
（F-k?2mg）d=

1

2

mv₂′²-

1

2

mv₁²，
挂接第二节车厢的过程中，动量守恒，
由动量守恒定律得：2mv₂′=3mv₂，
解得：v₂=

2 3 ( F m - 5 3 kg)d

，
挂接第三节车厢前，由动能定理得：
（F-k?3mg）d=

1

2

mv₃′²-

1

2

mv₂²，
挂接第三节车厢的过程中，动量守恒，
由动量守恒定律得：3mv₂′=4mv₃，
解得：v₃=

3 4 (F- 7 3 kg)d

，
同理可得，第n节车厢刚被带动时的速度：
v_n=

n n+1 (F- 2n+1 3 kg)d

；
（3）要想使最后一节车厢也能被带动起来，
则v_n≥0，即

n n+1 (F- 2n+1 3 kg)d

≥0，

F

m

-

2n+1

3

kg≥0，
则F≥

2n+1

3

kmg；
答：（1）第一节车厢刚被带动时列车的速度为：

1 2 ( F m -kg)d

；
（2）最后一节车厢刚被带动时列车的速度为

n n+1 (F- 2n+1 3 kg)d

；
（3）要想使最后一节车厢也能被带动起来，机车牵引力F的最小值为

2n+1

3

kmg．

点评：应用动能定理与动量守恒定律即可正确解题，解题时注意数学归纳法的应用．