题目内容
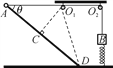
【题目】如图所示,重球用细绳跨过轻小光滑滑轮与小球相连,细绳处于水平拉直状态。小球由静止释放运动到最低点过程中,重球始终保持静止,不计空气阻力。下列说法正确的有( )

A. 细绳偏离竖直方向成θ角时,细绳拉力为mgcosθ
B. 地面对重球的摩擦力一直增大
C. 上述过程中小球重力的功率先增大后减小
D. 细绳对小球不做功
【答案】BCD
【解析】
设绳子与竖直方向的夹角为θ时绳子的拉力大小为T,根据牛顿第二定律得:T-mgcosθ=m![]() ,解得:T=mgcosθ+m
,解得:T=mgcosθ+m![]() ,故A错误;随着θ减小,v增大,可以知道绳子拉力T不断增大,则地面对重球的摩擦力一直增大,故B正确;开始时小球竖直方向的分速度vy为零,小球到达最低点时竖直方向的分速度vy也为零,则知vy先增大后减小,重力瞬时功率为P=mgvy,所以小球重力的功率先增大后减小,故C正确;细绳的拉力始终小球的速度垂直,对小球不做功,故D正确。故选BCD。
,故A错误;随着θ减小,v增大,可以知道绳子拉力T不断增大,则地面对重球的摩擦力一直增大,故B正确;开始时小球竖直方向的分速度vy为零,小球到达最低点时竖直方向的分速度vy也为零,则知vy先增大后减小,重力瞬时功率为P=mgvy,所以小球重力的功率先增大后减小,故C正确;细绳的拉力始终小球的速度垂直,对小球不做功,故D正确。故选BCD。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目