题目内容
3.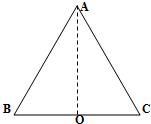 如图所示为一等边三角形的某种透明介质ABC,边长为L,折射率为$\frac{5}{3}$,底部中点O处有一点光源,试问能够从AB边射出光线的长度是多少?
如图所示为一等边三角形的某种透明介质ABC,边长为L,折射率为$\frac{5}{3}$,底部中点O处有一点光源,试问能够从AB边射出光线的长度是多少?
分析 根据临界角与折射率关系,求得临界角,再由等边三角形边长,结合几何关系,即可求得.
解答  解:根据临界角与折射率的关系,即 sinC=$\frac{1}{n}$=$\frac{3}{5}$
解:根据临界角与折射率的关系,即 sinC=$\frac{1}{n}$=$\frac{3}{5}$
解得:C=37°
等边三角形的边长为L,根据几何关系,则有OE=$\frac{\sqrt{3}}{4}L$
而EF=OEtanC=$\frac{3\sqrt{3}}{16}$L
x=BE+EF=$\frac{L}{4}$+$\frac{3\sqrt{3}}{16}$L
答:能够从AB边射出光线的长度是$\frac{L}{4}$+$\frac{3\sqrt{3}}{16}$L.
点评 考查光的全反射条件,掌握光的折射率与临界角的关系,理解几何关系的应用,注意正确画出光路图是解题的关键.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
14.一个质量为20kg的小孩从距地面高为3m,长为6m的滑梯顶端由静止开始滑下,滑到底端时的速度为2m/s,g=10m/s2,关于力对小孩做功说法正确的是( )
| A. | 重力做功1200J | B. | 合力做功40J | ||
| C. | 阻力做功为‐1160J | D. | 支持力做功40J |
11.许多物理学家在物理学的发展过程中做出了重要贡献,在物理史实和物理方法方面,下列表述正确的是( )
| A. | 牛顿通过实验研究了自由落体运动的规律 | |
| B. | 法拉第概括总结了法拉第电磁感应定律和判断感应电流方向的规律 | |
| C. | 比值定义法包括:电场强度E=$\frac{F}{q}$;电容C=$\frac{Q}{U}$;电阻R=$\frac{U}{I}$;加速度a=$\frac{F}{m}$ | |
| D. | 在牛顿发现万有引力定律的过程中,胡克曾给予了很大的帮助 |
18.滑块以速率v1冲上斜面,当它回到斜面底端时速率为v2,且v2<v1,若滑块向上运动的位移中点为A,取斜面底端重力势能为零,则( )
| A. | 上滑时机械能减小,下滑时机械能增大 | |
| B. | 上滑时机械能减小,下滑时机械能也减小 | |
| C. | 上滑过程中动能和重力势能相等的位置在A点上方 | |
| D. | 上滑过程中动能和重力势能相等的位置在A点下方 |
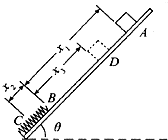 为测定物块与木板间的动摩擦因数,小明同学设计了如图所示的实验装置.木板的倾角为θ,弹簧的一端固定在木板上,另一端位于木板上的B点.物块在木板上A点静止释放后沿木板滑下,压缩弹簧运动至C点后被弹回,上滑至D点时速度为零.测得AB间的距离为x1、BC间的距离为x2,BD间的距离为x3.实验中的弹簧可视为轻质弹簧.
为测定物块与木板间的动摩擦因数,小明同学设计了如图所示的实验装置.木板的倾角为θ,弹簧的一端固定在木板上,另一端位于木板上的B点.物块在木板上A点静止释放后沿木板滑下,压缩弹簧运动至C点后被弹回,上滑至D点时速度为零.测得AB间的距离为x1、BC间的距离为x2,BD间的距离为x3.实验中的弹簧可视为轻质弹簧.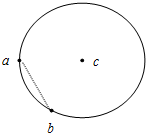 如图所示,半径为R的圆形区域,c为圆心,在圆上a点有一粒子源以相同的速率向圆面内各个方向发射多个质量为m、电荷量为+q 的带电粒子.当圆形区域存在垂直于圆面、磁感应强度大小为B的匀强磁场时,沿ac方向射入的粒子从b 点离开场区,此过程粒子速度方向偏转了$\frac{2π}{3}$.若只将圆形区域内的磁场换成平行于圆面的匀强电场,粒子从电场圆边界的不同位置射出时有不同的动能,其最大动能是初动能的4倍,经过b点的粒子在 b点的动能是初动能的3倍.不计粒子重力及粒子间的相互作用.求:
如图所示,半径为R的圆形区域,c为圆心,在圆上a点有一粒子源以相同的速率向圆面内各个方向发射多个质量为m、电荷量为+q 的带电粒子.当圆形区域存在垂直于圆面、磁感应强度大小为B的匀强磁场时,沿ac方向射入的粒子从b 点离开场区,此过程粒子速度方向偏转了$\frac{2π}{3}$.若只将圆形区域内的磁场换成平行于圆面的匀强电场,粒子从电场圆边界的不同位置射出时有不同的动能,其最大动能是初动能的4倍,经过b点的粒子在 b点的动能是初动能的3倍.不计粒子重力及粒子间的相互作用.求: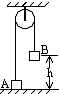 如图,跨过光滑的定滑轮的细线两端各系住物体A和B,已知两物体的质量分别是mA=0.1kg,mB=0.3kg,开始时将A用手揿住在地面上,放手后发现A能升起的最大高度为0.9m,问B物体原来离地面的高度h等于多少?
如图,跨过光滑的定滑轮的细线两端各系住物体A和B,已知两物体的质量分别是mA=0.1kg,mB=0.3kg,开始时将A用手揿住在地面上,放手后发现A能升起的最大高度为0.9m,问B物体原来离地面的高度h等于多少?