题目内容
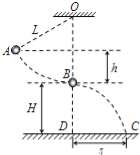
【题目】目前人类的火星之旅还面临着十大难题，其中之一是辐射问题，由于宇宙射线“风暴”常常会持续数日之久，前往火星探险的宇航员将面临遭受过量辐射的问题，为避免这一问题，科学家设想给航天器穿上一件“磁场外衣”，其过中心O的截面如图所示，匀强磁场分布在截面为环状的区域内，其内边界半径
，磁场方向垂直纸面向外，磁感应强度大小为B。设射线粒子带正电，质量为
，电荷量为
，最大速度为
，不计粒子的重力及相互间作用力.
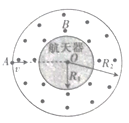
(1)若射线粒子从A点向O点以最大速度射入，请判断其圆周运动的旋转方向(“顺时针”或“逆时针”)，并求出轨迹半径
.
(2)要使第(1)题中粒子不能进人磁场内边界，则磁场外边界的半径
至少为多少?求此时粒子在磁场中的运动时间.
(3)在
为(2)中取值时，要使上述粒子从A点以任何方向入射都不能进入磁场内边界，匀强磁场的磁感应强度至少应调节到多少?
【答案】（1）r=a；（2）
（3）
【解析】（1）由左手定则可知，粒子做顺时针方向的圆周运动；
由洛伦兹力提供向心力得： 
，解得： 
=a。
（2）粒子运动轨迹如图甲所示。
由勾股定理得： 
，结合r=a，R1=a，则有： 
设圆周运动圆心角为
，由几何关系得： 
，得： 
粒子在磁场中运动时间： 
，结合周期：
得： 
（3）假设与磁场外边界相切的粒子恰好不进入保护区，所有的粒子都不能进入保护区，此时轨道如图乙所示，此粒子轨道半径： 
由
得： 
= 
练习册系列答案
相关题目
