��Ŀ����
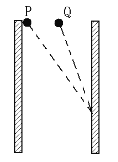
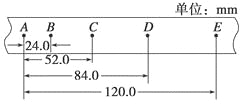
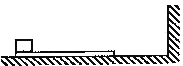
����Ŀ����ͼ��ʾ���⻬��ˮƽ������һľ�壬������˷���һ����ҷ���һ��ֱ��ǽ�����������Ϊľ��������2����������ľ���Ķ�Ħ������Ϊ��=0��2��ʹľ���������Թ�ͬ���ٶ�v0=6m/s�����˶���ijʱ��ľ����ǽ����������ײ����ײʱ�伫������֪ľ���㹻��������ʼ����ľ���ϣ��������ٶ�Ϊg=10m/s2
��ľ��ӵ�һ����ǽ��ײ���ڶ�����ǽ��ײ��������ʱ����
���𰸡�4s
��������
�����������һ����ǽ��ײ��ľ����ٶȷ���С���䣬�˺�ľ���������ȼ����˶��������������ȼ����˶������ľ�������ﵽ��ͬ���ٶ�v����ľ�������Ϊm�����������Ϊ2m��ȡ����Ϊ�����������ɶ����غ�ã�2mv0-mv0=3mv����
��ӵ�һ����ǽ��ײ�������ľ����й�ͬ�ٶ�v���õ�ʱ��Ϊt1����ľ��Ӧ�ö��������ã�
2��mgt1=mv-m��-v0������
��������ľ��������˶�ʱ�ļ��ٶ�Ϊa����ţ�ٵڶ����ɵã�2��mg=ma����
�ڴﵽ��ͬ�ٶ�vʱ��ľ����ǽ�ľ���lΪ��
l��v0t1![]() at12����
at12����
��ʼ�����������˶����ڶ�����ǽ��ײ��ʱ��Ϊ��![]() ����
����
�ӵ�һ����ײ���ڶ�����ײ��������ʱ��Ϊ��t=t1+t2����
�����ϸ�ʽ��![]()
�������ݿ�֪:t=4s