题目内容
1.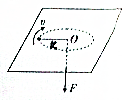 如图所示,在一块水平放置的光滑板中心开一个小孔,穿过一根细绳,细绳的一端用力F向下拉,另一端系一小球,使小球在板面上以半径R做匀速圆周运动,现开始缓慢地减小拉力,当拉力变为原来的四分之一时,小球仍做匀速圆周运动,半径变为2R,计算此过程中拉力对小球做的功.
如图所示,在一块水平放置的光滑板中心开一个小孔,穿过一根细绳,细绳的一端用力F向下拉,另一端系一小球,使小球在板面上以半径R做匀速圆周运动,现开始缓慢地减小拉力,当拉力变为原来的四分之一时,小球仍做匀速圆周运动,半径变为2R,计算此过程中拉力对小球做的功.
分析 物体在光滑水平面上做匀速圆周运动,由绳子的拉力提供向心力,根据牛顿第二定律分别求出两种拉力情况下物体的速度,再根据动能定理求出拉力对物体所做的功.
解答 解:设拉力为F时,小球做匀速圆周运动的线速度为v1,由牛顿第二定律得:F=m$\frac{{v}_{1}^{2}}{R}$,
当拉力为$\frac{1}{4}$F时,设小球做匀速圆周运动的线速度为v2,由牛顿第二定律得:$\frac{1}{4}$F=m$\frac{{v}_{2}^{2}}{2R}$,
小球运动半径由R变为2R过程中,由动能定理得,拉力对小球做的功为:W=$\frac{1}{2}$mv22-$\frac{1}{2}$mv12,
联立解得:W=-$\frac{1}{2}$FR;
答:拉力对小球做的功为-$\frac{1}{2}$FR.
点评 本题是向心力与动能定理的综合应用,要明确它们之间的纽带是速度.要知道细线的拉力提供物体圆周运动的向心力,明确动能定理是求变力做功常用的方法.

练习册系列答案
相关题目
16.一人造卫星在半径为R的轨道绕地球做匀速圆周运动,若该卫星在半径为2R的轨道上绕地球做匀速圆周运动,则( )
| A. | 卫星运动的线速度将增大到原来的2倍 | |
| B. | 卫星运动的线速度将减小到原来的$\frac{\sqrt{2}}{2}$ | |
| C. | 地球提供卫星的向心力将减小到原来的2倍 | |
| D. | 地球提供卫星的向心力将减小到原来的$\frac{1}{4}$ |
8.电荷是看不见的,但能被验电器检测出来是否存在.普通验电器顶部装有一个金属球,金属球与金属杆相连,在金属杆的底部是两片很薄的金属片.当验电器不带电荷时,金属片自然下垂.当一个带电体接触到金属球时,电荷能沿着金属棒传递,金属片就带有电荷.由于同时带有同一种电荷,两金属片相互排斥而张开.不管被检验的物体带负电还是正电,验电器的金属片都会张开.因此,这种验电器( )
| A. | 能用来直接判断电荷的正负 | B. | 不能用来直接判断电荷的正负 | ||
| C. | 可以用来间接判断电荷的正负 | D. | 可以直接测量物体的带电量 |

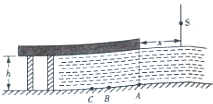 一湖面上有一伸向水面的混凝土观景台,如图所示是一截面图,观景台下表面恰好和水面相平,A为观景台右侧在湖底的投影,水深h=4m.在距观景台右侧面x=4m处有一可沿竖直方向上下移动的单色点光源S,点光源S可从距水面高3m处下移到接近水面,在移动过程中,观景台水下被照亮的最远距离为AC,最近距离为AB,若AB=3m,求:
一湖面上有一伸向水面的混凝土观景台,如图所示是一截面图,观景台下表面恰好和水面相平,A为观景台右侧在湖底的投影,水深h=4m.在距观景台右侧面x=4m处有一可沿竖直方向上下移动的单色点光源S,点光源S可从距水面高3m处下移到接近水面,在移动过程中,观景台水下被照亮的最远距离为AC,最近距离为AB,若AB=3m,求: 如图所示,光滑圆弧BC与水平面和传送带分别相切于B,C两点,圆弧所对应的圆心角θ=37°,圆弧BC的半径R=7m,足够长的传送带以恒定速率v=4m/s顺时针转动,传送带CD与水平面的夹角也为θ,一质量m=1kg的小滑块从A点以大小v0=10m/s的初速度向B点运动,A,B间的距离s=3.6m,已知小滑块与水平面、传送带之间的动摩擦因数均为μ=0.5,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,光滑圆弧BC与水平面和传送带分别相切于B,C两点,圆弧所对应的圆心角θ=37°,圆弧BC的半径R=7m,足够长的传送带以恒定速率v=4m/s顺时针转动,传送带CD与水平面的夹角也为θ,一质量m=1kg的小滑块从A点以大小v0=10m/s的初速度向B点运动,A,B间的距离s=3.6m,已知小滑块与水平面、传送带之间的动摩擦因数均为μ=0.5,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求: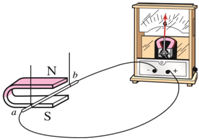 如图所示,是探究“什么情况下磁可以生电”的实验装置:
如图所示,是探究“什么情况下磁可以生电”的实验装置: 如图所示,一质量为m的小球,夹在斜面与竖直挡板之间保持静止,斜面倾角为30°,(不计一切摩擦).求:
如图所示,一质量为m的小球,夹在斜面与竖直挡板之间保持静止,斜面倾角为30°,(不计一切摩擦).求: