题目内容
(2007?茂名一模)某人造地球卫星质量为m,其绕地球运动的轨迹为椭圆,它在近地点时距地面高度为h1,速度为V1,加速度为
a1;在远地点时,距地面的高度为h2,速度为V2,加速度为a2.求:
(1)该卫星由远地点到近地点的过程中地球对它万有引力所做的功是多小?
(2)地球的半径是多少?
a1;在远地点时,距地面的高度为h2,速度为V2,加速度为a2.求:
(1)该卫星由远地点到近地点的过程中地球对它万有引力所做的功是多小?
(2)地球的半径是多少?
分析:(1)由远地点点到近地点点的过程只有万有引力做功,根据动能定理列式求解即可;
(2)万有引力提供向心力,根据牛顿第二定律两次列式后联立求解即可.
(2)万有引力提供向心力,根据牛顿第二定律两次列式后联立求解即可.
解答:解:(1)由动能定理得万有引力所做功
WG=
mv22-
mv12
(2)由万有引力定律等于向心力得
G
=ma1
G
=ma2
联立解得R=
解:(1)该卫星由远地点到近地点的过程中地球对它万有引力所做的功是
mv22-
mv12.
(2)地球的半径是
.
WG=
| 1 |
| 2 |
| 1 |
| 2 |
(2)由万有引力定律等于向心力得
G
| Mm |
| (R+h1)2 |
G
| Mm |
| (R+h2)2 |
联立解得R=
a2h1-
| ||
| a1-a2 |
解:(1)该卫星由远地点到近地点的过程中地球对它万有引力所做的功是
| 1 |
| 2 |
| 1 |
| 2 |
(2)地球的半径是
a2h1-
| ||
| a1-a2 |
点评:本题关键读懂题意,找出有用数据信息,然后根据牛顿第二定律列式后联立求解.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
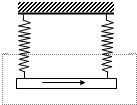 (2007?茂名一模)如图所示,用两个一样的弹簧测力计吊着一根铜棒,铜棒所在的虚线范围内有垂直纸面的匀强磁场,棒中通以自左向右的电流,当棒静止时,弹簧测力计的读数之和为F1;若将棒中的电流反向,当棒静止时,弹簧测力计的示数之和为F2,且F2>F1,根据这两个数据,可以确定( )
(2007?茂名一模)如图所示,用两个一样的弹簧测力计吊着一根铜棒,铜棒所在的虚线范围内有垂直纸面的匀强磁场,棒中通以自左向右的电流,当棒静止时,弹簧测力计的读数之和为F1;若将棒中的电流反向,当棒静止时,弹簧测力计的示数之和为F2,且F2>F1,根据这两个数据,可以确定( )