题目内容
3. 如图所示,斜面和水平面由一小段光滑圆弧连接,斜面的倾角为37°,一质量为0.5kg的物块从距斜面底端B点5m处的A点由静止释放.已知物块与水平面和斜面的动摩擦因数均为0.3.(sin37°=0.6,cos37°=0.8,g=10m/s2)
如图所示,斜面和水平面由一小段光滑圆弧连接,斜面的倾角为37°,一质量为0.5kg的物块从距斜面底端B点5m处的A点由静止释放.已知物块与水平面和斜面的动摩擦因数均为0.3.(sin37°=0.6,cos37°=0.8,g=10m/s2)(1)物块到达B点的速度为多大?
(2)物块在水平面上滑行的距离为多少?
(3)若物块开始静止在水平面上距B点10m的C点处,用大小为4.5N的水平恒力向右拉该物块,欲使物块能到达A点,水平恒力作用的最短距离为多大?
分析 (1)物块在斜面上做匀加速运动,在水平面上做匀减速运动,根据动能定理即可求解;
(2)从B到C,根据动能定理,即可求解;
(3)设力作用的最短距离,并由动能定理,即可求解
解答 解:(1)从A到B由动能定理得:
$\frac{1}{2}$mvB2=mgLsin37°-μmg cos37°L
得vB=6m/s
(2)从B到C由动能定理得:
$\frac{1}{2}$ mvC2-$\frac{1}{2}$mvB2=-μmgS
解得 S=6m
(3)设力作用的最短距离为S′,根据动能定理可得:
FS′-μmgS-mgLsin37°-μmgLcos37°=0
解得:S′=8m
答:(1)物块到达B点的速度为6m/s
(2)物块在水平面上滑行的距离为6m
(3)水平恒力作用的最短距离为8m
点评 考查牛顿第二定律与运动学公式的综合,掌握动能定理的应用,注意过程的选取,及力做功的正负

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.一列简谐横波,在t=0.6s时刻的图象如图甲所示,波上A质点的振动图象如图乙所示,则以下说法正确的是( )


| A. | 这列波沿x轴正方向传播,波速是$\frac{50}{3}$m/s | |
| B. | 从t=0.6s开始,紧接着的△t=0.6s时间内,A质点通过的路程是4m | |
| C. | 从t=0.6s开始,质点P比质点Q早0.4s到达波峰位置 | |
| D. | 从t=0.6s开始,再经0.15s质点Q第一次到达波谷位置 |
11. 光滑绝缘曲面与竖直平面的交线是抛物线,如图所示,抛物线的方程是y=x2,下半部处在一个水平方向的匀强磁场中,磁场的上边界是y=a的直线(图中的虚线所示),一个质量为m的小金属球从抛物线上y=b(b>a)处沿抛物线自由下滑,忽略空气阻力,重力加速度值为g.则( )
光滑绝缘曲面与竖直平面的交线是抛物线,如图所示,抛物线的方程是y=x2,下半部处在一个水平方向的匀强磁场中,磁场的上边界是y=a的直线(图中的虚线所示),一个质量为m的小金属球从抛物线上y=b(b>a)处沿抛物线自由下滑,忽略空气阻力,重力加速度值为g.则( )
 光滑绝缘曲面与竖直平面的交线是抛物线,如图所示,抛物线的方程是y=x2,下半部处在一个水平方向的匀强磁场中,磁场的上边界是y=a的直线(图中的虚线所示),一个质量为m的小金属球从抛物线上y=b(b>a)处沿抛物线自由下滑,忽略空气阻力,重力加速度值为g.则( )
光滑绝缘曲面与竖直平面的交线是抛物线,如图所示,抛物线的方程是y=x2,下半部处在一个水平方向的匀强磁场中,磁场的上边界是y=a的直线(图中的虚线所示),一个质量为m的小金属球从抛物线上y=b(b>a)处沿抛物线自由下滑,忽略空气阻力,重力加速度值为g.则( )| A. | 小金属球沿抛物线下滑后最终停在O点 | |
| B. | 小金属球沿抛物线下滑后每次过O点速度一直在减小 | |
| C. | 小金属球沿抛物线下滑后对O点压力一定大于mg | |
| D. | 小金属球沿抛物线下滑后最终产生的焦耳热总量是mg(b-a) |
18. 质量为m的小物块在倾角为α的斜面上处于静止状态,如图所示.若斜面体和小物块一起以速度v沿水平方向向右做匀速直线运动,通过一段位移s.斜面体对物块的摩擦力和支持力的做功情况是( )
质量为m的小物块在倾角为α的斜面上处于静止状态,如图所示.若斜面体和小物块一起以速度v沿水平方向向右做匀速直线运动,通过一段位移s.斜面体对物块的摩擦力和支持力的做功情况是( )
 质量为m的小物块在倾角为α的斜面上处于静止状态,如图所示.若斜面体和小物块一起以速度v沿水平方向向右做匀速直线运动,通过一段位移s.斜面体对物块的摩擦力和支持力的做功情况是( )
质量为m的小物块在倾角为α的斜面上处于静止状态,如图所示.若斜面体和小物块一起以速度v沿水平方向向右做匀速直线运动,通过一段位移s.斜面体对物块的摩擦力和支持力的做功情况是( )| A. | 摩擦力做正功,支持力做正功 | B. | 摩擦力做正功,支持力做负功 | ||
| C. | 摩擦力做负功,支持力做正功 | D. | 摩擦力做负功,支持力做负功 |
8.如图所示,A、B是相同的白炽灯,L是自感系数很大、电阻可忽略的自感线圈.下面说法正确的是( )


| A. | 闭合开关S时,A、B灯同时亮,且达到正常 | |
| B. | 闭合开关S时,B灯比A灯先亮,最后一样亮 | |
| C. | 闭合开关S时,A灯比B灯先亮,最后一样亮 | |
| D. | 断开开关S时,A、B灯同时熄灭 |
15. 如图所示,小钢球m以初速度v0在光滑水平面上运动,后受到磁极的侧向作用力而作图示的曲线运动到达D点,由图可知磁极的位置及极性可能是( )
如图所示,小钢球m以初速度v0在光滑水平面上运动,后受到磁极的侧向作用力而作图示的曲线运动到达D点,由图可知磁极的位置及极性可能是( )
 如图所示,小钢球m以初速度v0在光滑水平面上运动,后受到磁极的侧向作用力而作图示的曲线运动到达D点,由图可知磁极的位置及极性可能是( )
如图所示,小钢球m以初速度v0在光滑水平面上运动,后受到磁极的侧向作用力而作图示的曲线运动到达D点,由图可知磁极的位置及极性可能是( )| A. | 磁极在A位置,极性一定是N极 | B. | 磁极在B位置,极性一定是S极 | ||
| C. | 磁极在C位置,极性一定是N极 | D. | 磁极在B位置,极性无法确定 |
12.质量为m的物体受到一组共点恒力作用而处于平衡状态,当撤去某个恒力F1时,物体不可能做( )
| A. | 匀加速直线运动 | B. | 匀减速直线运动 | C. | 匀变速曲线运动 | D. | 匀速直线运动 |
13.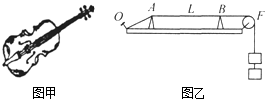 弦乐器小提琴是由两端固定的琴弦产生振动而发音的,如图甲所示,为了研究同一根琴弦振动频率与哪些因素有关,可利用如图乙所示的实验装置,一块厚木板上有AB两个楔支撑着琴弦,其中A楔固定,B楔可沿木板移动来改变琴弦振动部分的长度,将琴弦的末端固定在木板O点,另一端通过滑轮接上砝码以提供一定拉力,轻轻拨动琴弦,在AB间产生振动.
弦乐器小提琴是由两端固定的琴弦产生振动而发音的,如图甲所示,为了研究同一根琴弦振动频率与哪些因素有关,可利用如图乙所示的实验装置,一块厚木板上有AB两个楔支撑着琴弦,其中A楔固定,B楔可沿木板移动来改变琴弦振动部分的长度,将琴弦的末端固定在木板O点,另一端通过滑轮接上砝码以提供一定拉力,轻轻拨动琴弦,在AB间产生振动.
(1)先保持拉力为150N不变,改变AB的距离L(即改变琴弦长度),测出不同长度时琴弦振动的频率,记录结果如表1所示.
从表1数据可判断在拉力不变时,琴弦振动的频率f与弦长L的关系为频率f与弦长L成反比.
(2)保持琴弦长度为0.80m不变,改变拉力,测出不同拉力时琴弦振动的频率,记录结果如表2所示.
从表2数据可判断在琴弦长度不变时,琴弦振动的频率f与拉力F的关系为频率f与拉力F的平方根成正比.
(3)如果在相同的环境中研究不同种类的小提琴琴弦,除了长度L和拉力F以外,你认为还有哪些因素会影响琴弦振动的频率?试列举可能的一个因素:弦的半径(即直径、粗细等)或弦的材料(即密度、单位长度的质量等.
 弦乐器小提琴是由两端固定的琴弦产生振动而发音的,如图甲所示,为了研究同一根琴弦振动频率与哪些因素有关,可利用如图乙所示的实验装置,一块厚木板上有AB两个楔支撑着琴弦,其中A楔固定,B楔可沿木板移动来改变琴弦振动部分的长度,将琴弦的末端固定在木板O点,另一端通过滑轮接上砝码以提供一定拉力,轻轻拨动琴弦,在AB间产生振动.
弦乐器小提琴是由两端固定的琴弦产生振动而发音的,如图甲所示,为了研究同一根琴弦振动频率与哪些因素有关,可利用如图乙所示的实验装置,一块厚木板上有AB两个楔支撑着琴弦,其中A楔固定,B楔可沿木板移动来改变琴弦振动部分的长度,将琴弦的末端固定在木板O点,另一端通过滑轮接上砝码以提供一定拉力,轻轻拨动琴弦,在AB间产生振动.(1)先保持拉力为150N不变,改变AB的距离L(即改变琴弦长度),测出不同长度时琴弦振动的频率,记录结果如表1所示.
| 长度大小L/m | 1.00 | 0.75 | 0.50 | 0.25 |
| 振动频率f/Hz | 150 | 200 | 300 | 600 |
(2)保持琴弦长度为0.80m不变,改变拉力,测出不同拉力时琴弦振动的频率,记录结果如表2所示.
| 拉力大小F/N | 400 | 225 | 144 | 100 | 25 |
| $\sqrt{F}$大小 | 20 | 15 | 12 | 10 | 5 |
| 振动频率f/Hz | 305 | 229 | 183 | 153 | 76 |
(3)如果在相同的环境中研究不同种类的小提琴琴弦,除了长度L和拉力F以外,你认为还有哪些因素会影响琴弦振动的频率?试列举可能的一个因素:弦的半径(即直径、粗细等)或弦的材料(即密度、单位长度的质量等.
 如图所示,固定在匀强磁场中的水平导轨ab、cd的间距为L1=0.5m,金属棒ad与导轨左端bc的距离为L2=0.8m,整个闭合回路的电阻为R=0.2Ω,磁感应强度为B0=1T的匀强磁场竖直向下穿过整个回路.ad杆通过滑轮和轻绳连接着一个质量为m=0.04kg的物体,不计一切摩擦,现使磁场以$\frac{△B}{△t}$=0.2T/s的变化率均匀地增大.取g=10m/s2.试求:
如图所示,固定在匀强磁场中的水平导轨ab、cd的间距为L1=0.5m,金属棒ad与导轨左端bc的距离为L2=0.8m,整个闭合回路的电阻为R=0.2Ω,磁感应强度为B0=1T的匀强磁场竖直向下穿过整个回路.ad杆通过滑轮和轻绳连接着一个质量为m=0.04kg的物体,不计一切摩擦,现使磁场以$\frac{△B}{△t}$=0.2T/s的变化率均匀地增大.取g=10m/s2.试求: