题目内容
环型对撞机是研究高能粒子的重要装置，带电粒子在电压为U的电场中加速后注入对撞机的高真空圆形状的空腔内，在匀强磁场中，做半径恒定的圆周运动，且局限在圆环空腔内运动，粒子碰撞时发生核反应，关于带电粒子的比荷
，加速电压U和磁感应强度B以及粒子运动的周期T的关系，下列说法正确的是（ ）
| q |
| m |
分析：带电粒子在电场中被加速后，进入匀强磁场后做匀速圆周运动．由题知，带电粒子圆周运动的半径都相同，
则由半径公式与粒子在电场中加速公式：
mv2=qU，研究粒子的比荷和磁感应强度、周期的关系．
则由半径公式与粒子在电场中加速公式：
| 1 |
| 2 |
解答：解：带电粒子在匀强磁场中做匀速圆周运动，由洛伦兹力提供向心力可知：Bqv=m
，解得：R=
…①
而粒子在电场中被加速，则有：
mv2=qU…②
由①②得：R=
?
，带电粒子运行的周期T=
根据这两个表达式可知：
A、对于给定的加速电压，带电粒子的比荷
越大，磁感应强度B越小，故A错误，B正确；
C、对于给定的带电粒子，不管加速电压U多大，粒子运动的周期T都不变，故C错误，D正确．
故选BD
| v2 |
| R |
| mv |
| Bq |
而粒子在电场中被加速，则有：
| 1 |
| 2 |
由①②得：R=
| ||
| B |
|
| 2πm |
| Bq |
根据这两个表达式可知：
A、对于给定的加速电压，带电粒子的比荷
| q |
| m |
C、对于给定的带电粒子，不管加速电压U多大，粒子运动的周期T都不变，故C错误，D正确．
故选BD
点评：本题通过洛伦兹力提供向心力来导出半径公式与周期公式，再用动能定理得出粒子在电场中的加速公式，从而可推导出加速电压、磁感应强度、粒子的比荷及半径的关系．最终由控制变量来研究其它各量之间的具体关系．
练习册系列答案
快捷英语周周练系列答案
相关题目
（2013?德阳模拟）环型对撞机是研究高能粒子的重要装置．正、负离子由静止经过电压U的直线加速器加速后，沿圆环切线方向注入对撞机的真空环状空腔内，空腔内存在着与圆环平面垂直的匀强磁场，磁感应强度大小为B．两种带电粒子将被局限在环状空腔内，沿相反方向做半径相等的匀速圆周运动，从而在碰撞区迎面相撞．为维持带电粒子在环状空腔中的匀速圆周运动，下列说法正确的（ ）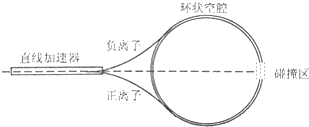
在粒子加速领域中A．有开创贡献的物理学家谢家麟获得2011年度国家最高科学技术奖，该奖项被誉为是“中国的诺贝尔奖”．谢家麟在上世纪80年代参勾了北京正负电子环艰对撞机的研究．环型对撞机是研究高能粒子的重耍装S，比荷相等的正、负离子由静止都经过电压为U的直线加速器加速后，沿圆环切线方向同时注入对撞机的高其空环状空腔内，空腔内存在着与圆环平面乖直的匀强磁场，磁感应强度人小为B．正、负离子在环状空腔内只受洛伦兹力作用而沿相反方向做半径相等的匀速圆周运动，然后在碰撞区迎面相撞，不考虑相对论效应，下列说法正确的是（ ）环型对撞机是研究高能粒子的重要装置，其核心部件是一个高真空的圆环状的空腔．若带电粒子初速可视为零，经电压为U的电场加速后，沿圆环切线方向注入对撞机的环状空腔内，空腔内存在着与圆环平面垂直的匀强磁场，磁感应强度大小为B．带电粒子将被限制在圆环状空腔内运动．要维持带电粒子在圆环内做半径确定的圆周运动，下列说法中正确的是（ ）
| A、对于给定的加速电压，带电粒子的比荷q/m越大，磁感应强度B越大 | B、对于给定的加速电压，带电粒子的比荷q/m越大，磁感应强度B越小 | C、对于给定的带电粒子，加速电压U越大，粒子运动的周期越小 | D、对于给定的带电粒子，不管加速电压U多大，粒子运动的周期都不变 |