题目内容
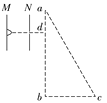
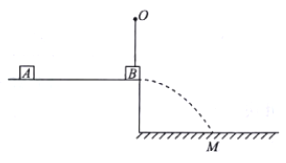
【题目】如图所示，质量为0.2kg的小物块B用不可伸长的细绳悬挂于O点，静止时恰好位于0.8m高的光滑平台的右端，质量为0.4kg的小物块A以2m/s的初速度向右运动并与小物块B发生对心碰撞，碰后小物块A滑下平台落于水平面上M点，水平射程为0.48m，已知碰后小物块B运动过程中细绳不松弛且小物块B运动至最高点时动能为0，小物块A、B均可视为质点，重力加速度g=10m/s2，求：
（1）小物块A、B碰撞过程中损失的机械能；
（2）细绳的长度应满足什么条件；若要求小物块B对细绳的拉力最大，则此时的绳长和最大拉力分别为多少。
【答案】（1）0.256J（2） 0.128m ，6N
【解析】试题分析：由平抛运动，可求小物块A的水平速度，结合动量守恒定律及能量守恒定律可求小物块A、B碰撞过程中损失的机械能；当小物块B运动到最高点时
时，拉力最大，由牛顿第二定律即可求解。
（1)小物块A滑下平台后做平抛运动，竖直方向
，解得t=0.4s
水平方向
，解得vA=1.2m/s
小物块A、B碰撞过程由动量守恒定律得
由能量守恒定律得
解得
（2）碰后小物块B运动过程中细绳不松弛且小物块B运动至最高点时动能为0，则小物块B最高能摆
至与圆心等高，此时细绳长度最小，由机械能守恒定律得
解得l=0.128m
故细绳长度应大于等于0.128m
小物块B在最低点时对细绳拉力最大，在最低点由牛顿第二定律得
可知绳长最短时，拉力最大，此时绳长为0.128m
拉力T=6N
练习册系列答案
相关题目
