Question

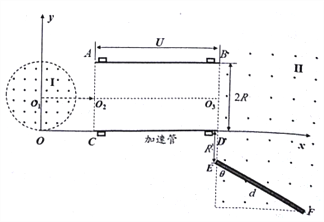
【题目】如图所示，半径为R的圆形匀强磁场区域Ⅰ与x轴相切于坐标系的原点O，磁感应强度为，方向垂直于纸面向外，磁场区域Ⅰ右侧有一长方体加速管，加速管底面宽度为2R，轴线与x轴平行且过磁场区域Ⅰ的圆心，左侧的电势比右侧高.在加速管出口正下方距离D点为R处放置一宽度为d=3R的荧光屏EF，荧光屏与竖直方向成θ=60°角，加速管右侧存在方向垂直于纸面向外的匀强磁场区域Ⅱ，磁感应强度为.在0点处有一个粒子源，能沿纸面向y>0的各个方向均匀地发射大量质量为m带电荷量为q且速率相同的粒子，其中沿y轴正方向射入磁场的粒子，恰能沿轴线O2O3进入长方形加速管并垂直打在荧光屏上，(不计粒子重力及其相互作用).

(1)求粒子刚进入加速管时的速度n的大小和加速电压U；

(2)求荧光屏上被粒子打中的区域长度Δl；

(3)若要让从加速管BO3区域出来的粒子全部打中荧光屏，磁场Ⅱ的磁感应强度大小应满足什么条件?

Answer 1

【答案】（1）（2）R（3）≤B≤

【解析】试题分析：粒子在磁场Ⅰ中，根据洛伦兹力提供向心力，求出速度，粒子在加速管中作加速运动，由动能定理求出加速电压U；从B点穿出的粒子打在离E点最近的屏上，画出粒子运动轨迹，由几何关系得即可求出荧光屏上被粒子打中的区域长度；画出粒子运动轨迹，由几何关系和圆周运动公式即可求出磁感应强度满足的范围。

（1）粒子在磁场Ⅰ中的运动半径为R，如图所示：

由向心力公式可得：

解得：

因粒子垂直打在荧光屏上，由题意可知，如图：

在磁场Ⅱ中的运动半径为2R，

由向心力公式可得：

解得：

粒子在加速管中作加速运动，由动能定理得：

联立解得加速管所加的电压为：

(2)从B点穿出的粒子打在离E点最近的屏上，如图所示：

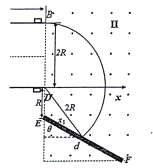
由几何关系得：

解得：

从D点穿出的粒子打在离E 点最远的屏上，如图所示：

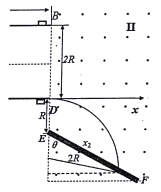
由几何关系得：

解得：

粒子打中的区域长度

(3)从O3点穿出的粒子恰好打在F点时，如图所示：

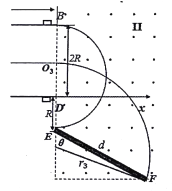
有几何关系可得：

解得：

由向心力公式有：

联立解得：

从B点穿出的粒子恰好打在E 点时，有：

由向心力公式有：

联立解得：

从BO3区域穿出的粒子打在粒子全部打在屏上磁感应强度大小满足的条件是： ≤B≤。