题目内容
如甲图所示,水平光滑地面上用两颗钉子(质量忽略不计)固定停放着一辆质量为M=3kg的小车,小车的四分之一圆弧轨道是光滑的,半径为R=0.5m,在最低点B与水平轨道BC相切,视为质点的质量为m=1kg的物块从A点正上方距A点高为h=0.3m处无初速下落,恰好落入小车圆弧轨道滑动,然后沿水平轨道滑行恰好停在轨道末端C。
现去掉钉子(水平面依然光滑未被破坏)不固定小车,而让其左侧靠在竖直墙壁上,该物块仍从原高度处无初速下落,如乙图所示。
不考虑空气阻力和物块落入圆弧轨道时的能量损失,已知物块与水平轨道BC间的动摩擦因数为μ=0.2

求:(1)水平轨道BC长度;
(2)小车固定时物块到达圆弧轨道最低点B时对轨道的压力;
(3)小车不固定时物块再次停在小车上时距小车B点的距离;
(4)两种情况下由于摩擦系统产生的热量之比。
现去掉钉子(水平面依然光滑未被破坏)不固定小车,而让其左侧靠在竖直墙壁上,该物块仍从原高度处无初速下落,如乙图所示。
不考虑空气阻力和物块落入圆弧轨道时的能量损失,已知物块与水平轨道BC间的动摩擦因数为μ=0.2

求:(1)水平轨道BC长度;
(2)小车固定时物块到达圆弧轨道最低点B时对轨道的压力;
(3)小车不固定时物块再次停在小车上时距小车B点的距离;
(4)两种情况下由于摩擦系统产生的热量之比。
(1)4m (2)42N (3)3m (4)4:3
试题分析:(1)根据动能定理可得
 ,解得
,解得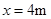 。
。(2)物块到达B点的速度为
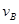 ,
,根据机械能守恒有
 ,
,解得
 ,
,在B点,合外力等于向心力,即

解得
 ,根据牛顿第三定律可得小车固定时物块到达圆弧轨道最低点B时对轨道的压力为42N。
,根据牛顿第三定律可得小车固定时物块到达圆弧轨道最低点B时对轨道的压力为42N。(3)到达B点前小车不动,系统当物块到达B点以后的运动动量守恒,最终二者速度相同
所以
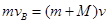 解得
解得
此过程中物块的加速度大小
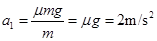
小车的加速度大小

速度相等时物块的位移由
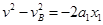 ,解得
,解得
速度相等时小车的位移由
 ,解得
,解得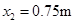
小车不固定时物块再次停在小车上时距小车B点的距离

(4)小车固定时摩擦系统产生的热量
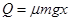 ,小车不固定时摩擦系统产生的热量
,小车不固定时摩擦系统产生的热量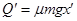 ,所以
,所以
点评:本题(3)还可以根据系统损失的机械能等于系统产生的热来计算小车不固定时物块再次停在小车上时距小车B点的距离,即
 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
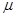 ,重力加速度为g,以下判断正确的是
,重力加速度为g,以下判断正确的是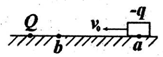
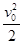
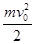
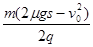

 +mgh
+mgh




