Question

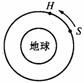
一组航天员乘坐飞船，去修理位于离地球表面6.0×10⁵m的圆形轨道上的哈勃太空望远镜H。机组人员使穿梭机S进入与H相同的轨道并关闭推动火箭，而望远镜则在穿梭机前方数公里处，如右图所示。（已知地球半径为R＝6.4×10⁶ m，地球质量为M＝6.0×10²⁴ kg，引力常数为G＝6.67×10^－11  Nm²/kg²）
（1）在穿梭机内，一质量为70kg的航天员的视重是多少？
（2）①计算轨道上的重力加速度的值；
②计算穿梭机在轨道上的速率和周期。
（3）在如右图所示位置，穿梭机要追上前面的太空望远镜，则应该怎样运动？

Answer 1

（14分）解：（1）视重为0 （3分）（2）①因为mg’＝G，所以g’＝G，（1分）代入数据得：g’＝8.2 m/s²，（1分）②地球对穿梭机的万有引力提供向心力，有G＝m， 所以v＝＝m/s＝7651 m/s，（2分） T＝2p＝2ps＝5817 s，（2分）（3）穿梭机应首先减少其原有速率进入半径较小的轨道（1分），因引力做正功，动能增加（1分），低轨道环绕速度大于原轨道的环绕速度，同时具有较大的角速度（1分），最后，穿梭机在低轨道上加速进入半径较大的原轨道追上前面的望远镜（1分）。