题目内容
(08年四川卷)(20分) 一倾角为θ=45°的斜血固定于地面,斜面顶端离地面的高度h0=1m,斜面底端有一垂直于斜而的固定挡板。在斜面顶端自由释放一质量m=0.09kg的小物块(视为质点)。小物块与斜面之间的动摩擦因数μ=0.2。当小物块与挡板碰撞后,将以原速返回。重力加速度g=10 m/s2。在小物块与挡板的前4次碰撞过程中,挡板给予小物块的总冲量是多少?
一倾角为θ=45°的斜血固定于地面,斜面顶端离地面的高度h0=1m,斜面底端有一垂直于斜而的固定挡板。在斜面顶端自由释放一质量m=0.09kg的小物块(视为质点)。小物块与斜面之间的动摩擦因数μ=0.2。当小物块与挡板碰撞后,将以原速返回。重力加速度g=10 m/s2。在小物块与挡板的前4次碰撞过程中,挡板给予小物块的总冲量是多少?
解析:
解法一:
设小物块从高为h处由静止开始沿斜面向下运动,到达斜面底端时速度为v。
由功能关系得
![]() ①
①
以沿斜面向上为动量的正方向。按动量定理,碰撞过程中挡板给小物块的冲量
![]() ②
②
设碰撞后小物块所能达到的最大高度为h’,则
![]() ③
③
同理,有
![]() ④
④
![]() ⑤
⑤
式中,v’为小物块再次到达斜面底端时的速度,I’为再次碰撞过程中挡板给小物块的冲量。由①②③④⑤式得
![]() ⑥
⑥
式中 ![]() ⑦
⑦
由此可知,小物块前4次与挡板碰撞所获得的冲量成等比级数,首项为
![]() ⑧
⑧
总冲量为
![]() ⑨
⑨
由 ![]() ⑩
⑩
得 ![]()
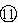
代入数据得 ![]() N?s
N?s 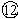
解法二:
设小物块从高为h处由静止开始沿斜面向下运动,小物块受到重力,斜面对它的摩擦力和支持力,小物块向下运动的加速度为a,依牛顿第二定律得
![]() ①
①
设小物块与挡板碰撞前的速度为v,则
![]() ②
②
以沿斜面向上为动量的正方向。按动量定理,碰撞过程中挡板给小物块的冲量为
![]() ③
③
由①②③式得
![]() ④
④
设小物块碰撞后沿斜面向上运动的加速度大小为a’, 依牛顿第二定律有
![]() ⑤
⑤
小物块沿斜面向上运动的最大高度为
![]() ⑥
⑥
由②⑤⑥式得 ![]() ⑦
⑦
式中 ![]() ⑧
⑧
同理,小物块再次与挡板碰撞所获得的冲量
![]() ⑨
⑨
由④⑦⑨式得 ![]() ⑩
⑩
由此可知,小物块前4次与挡板碰撞所获得的冲量成等比级数,首项为
![]()
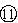
总冲量为 ![]()
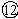
由 ![]()
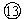
得 ![]()
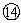
代入数据得 ![]() N?s
N?s 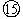

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
 一质量为M的探空气球在匀速下降,若气球所受浮力F始终保持不变,气球在运动过程中所受阻力仅与速率有关,重力加速度为g。现欲使该气球以同样速率匀速上升,则需从气球吊篮中减少的质量为
一质量为M的探空气球在匀速下降,若气球所受浮力F始终保持不变,气球在运动过程中所受阻力仅与速率有关,重力加速度为g。现欲使该气球以同样速率匀速上升,则需从气球吊篮中减少的质量为
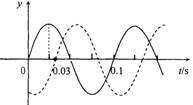 (08年四川卷)一列简谐横波沿直线传播,该直线上的a、b两点相距4.42 m。图中实、虚两条曲线分别表示平衡位置在a、b两点处质点的振动曲线。从图示可知
(08年四川卷)一列简谐横波沿直线传播,该直线上的a、b两点相距4.42 m。图中实、虚两条曲线分别表示平衡位置在a、b两点处质点的振动曲线。从图示可知