题目内容
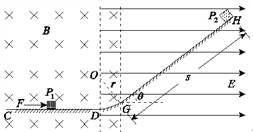
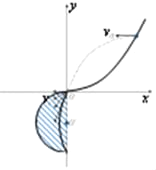
【题目】在竖直面内建立直角坐标系,曲线![]() 位于第一象限的部分如图,在曲线上不同点以初速度v0向x轴负方向水平抛出质量为m,带电量为+q的小球,小球下落过程中都会通过坐标原点,之后进入第三象限的匀强电场和匀强磁场区域,磁感应强度为
位于第一象限的部分如图,在曲线上不同点以初速度v0向x轴负方向水平抛出质量为m,带电量为+q的小球,小球下落过程中都会通过坐标原点,之后进入第三象限的匀强电场和匀强磁场区域,磁感应强度为![]() ,方向垂直纸面向里,小球恰好做匀速圆周运动,并在做圆周运动的过程中都能打到y轴负半轴上(已知重力加速度为g=10m/s2、
,方向垂直纸面向里,小球恰好做匀速圆周运动,并在做圆周运动的过程中都能打到y轴负半轴上(已知重力加速度为g=10m/s2、![]() ).求:
).求:
(1)第三象限的电场强度大小及方向;
(2)沿水平方向抛出的初速度v0;
(3)为使所有的小球都打到y轴负半轴,所加磁场区域的最小面积.
【答案】(1)0.1N/C,方向:竖直向上(2)10m/s(3)0.5m2
【解析】试题分析:(1)小球在第三象限做匀速圆周运动,说明受到的合外力提供向心加速度,即洛伦兹力提供向心加速度,由此即可得出电场力与重力大小相等方向相反;
(2)小球在电场中做类平抛运动,应用类平抛运动规律可以求出小球的速度;
(3)分析小球在电场中运动的可能的情况,结合矢量的分解的方法,求出粒子进入磁场时的速度方向与初速度、末速度的关系,得出半径与偏转距离的关系,从而得出磁场的长度和宽度,即可求出磁场区域的最小面积.
(1)小球做匀速圆周运动,重力与电场力合力为零,即![]() ,
,
解得![]() ,方向:竖直向上;
,方向:竖直向上;
(2)小球在电场中做类平抛运动,
水平方向: ![]() ,
,
竖直方向: ![]() ,
,
由题意可知: ![]() ,
,
解得: ![]() ;
;
(3)设小球进入第三象限时的速度为v,与x轴负方向夹角为α,则![]() ,
,
小球在磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得![]() ,
,
解得: ![]() ,
,
小球打在y轴的点与原点的距离: ![]() ,
,
所有小球均从y轴负半轴上同一点进入第四象限,
最小磁场区域为一半径为![]() 的半圆,
的半圆,
磁场面积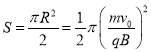 ,
,
解得,磁场最小面积: ![]() ;
;

练习册系列答案
相关题目