题目内容
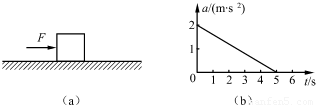
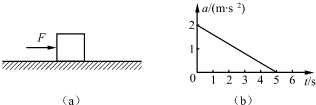
利用图象可以描述两个物理量之间的关系,图象除了能直接表明这两个物理量之间的变化特点外,图线与横轴所围的面积还可以表示第三个物理量.例如:在v-t图象中,图线与横轴所围的面积为物体在这段时间内的位移x.如图(a)所示,质量为1kg的物块,在水平向右、大小为5N的恒力F作用下,沿粗糙水平面由静止开始运动.在运动过程中,物块受到水平向左的空气阻力,其大小随着物块速度的增大而增大,且当物块速度为零时,空气阻力也为零.物块加速度a与时间t的关系图线如图(b)所示,求:
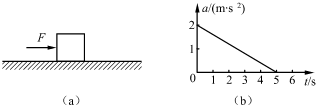
(1)物块与水平面间的动摩擦因数μ;
(2)t=5s时物块速度的大小;
(3)t=6s时空气阻力的大小.
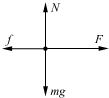 解:(1)当t=0时,由题意可知,物体所受空气阻力为零,此时物块的受力情况如图所示.由牛顿第二定律有:
解:(1)当t=0时,由题意可知,物体所受空气阻力为零,此时物块的受力情况如图所示.由牛顿第二定律有:F-f=ma0①
N-mg=0②
又因为 f=μN③
由①②③可求得:μ=0.3
(2)由题意可知,在a-t图中,图线与t轴所围的面积为速度的增加量,
所以t=5s时物块的速度
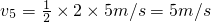
(3)由图象可知,t=5s后,物块做匀速直线运动,物体所受的空气阻力不变,设此过程中物块所受空气阻力为F空,
由牛顿第二定律有:F-f-F空=0④
由②③④式可求得:F空=2N
答:(1)物块与水平面间的动摩擦因数为0.3.
(2)t=5s时物块速度的大小为5m/s.
(3)t=6s时空气阻力的大小为2N.
分析:(1)初始时刻,速度为零,空气阻力为零,根据牛顿第二定律求出物块与水平面间的动摩擦因数.
(2)加速度a与时间t的关系图线围成的面积表示速度的变化量,根据图象求出t=5s时物块速度的大小.
(3)t=5s后,物块做匀速直线运动,物体所受的空气阻力不变,根据平衡求出空气阻力的大小.
点评:解决本题的关键能够正确地受力分析,运用牛顿第二定律和共点力平衡求解.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
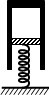 ,弹簧一端固定于水平面上,另一端与质量为m的活塞拴接在一起,开口向下、质量为M的气缸与活塞一起封闭了一定质量的气体.气缸和活塞均可与外界进行热交换.若外界环境的温度缓慢降低,则封闭气体的体积将
,弹簧一端固定于水平面上,另一端与质量为m的活塞拴接在一起,开口向下、质量为M的气缸与活塞一起封闭了一定质量的气体.气缸和活塞均可与外界进行热交换.若外界环境的温度缓慢降低,则封闭气体的体积将