题目内容
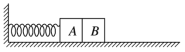
【题目】如图所示,质量均为m=2.0kg的物块A、B紧挨着放置在粗糙的水平地面上,物块A的左侧连接一劲度系数为k=100 N/m的轻质弹簧,弹簧另一端固定在竖直墙壁上。开始时,两物块压紧弹簧并都恰好处于静止状态。现使物块B在水平外力F(图中未画出)作用下向右做加速度大小为a=2m/s2的匀加速直线运动直至与A分离,已知两物块与地面间的动摩擦因数均为μ=0.4,最大静摩擦力等于滑动摩擦力,不计空气阻力,g=10 m/s2.则( )
A. 开始时,弹簧的压缩量大小为8 cm
B. 物块A、B分离时,所加外力F的大小为24 N
C. 物块A、B由静止开始运动到分离所用的时间为0.4 s
D. 物块A、B由静止开始运动到分离时,物块A的位移大小为4 cm
【答案】D
【解析】
A.开始时,两物块压紧弹簧并恰好处于静止状态,根据平衡条件可得:
kx0=μ2mg
解得:
x0=0.16m=16cm
故A错误;
B.物块A、B分离时,此时A和B之间的弹力为零,以B为研究对象,根据牛顿第二定律可得:
F-μmg=ma
解得所加外力
F=12N
故B错误;
CD.以A为研究对象,分离时弹簧压缩量为x,则
kx-μmg=ma
解得
x=0.12m
此过程A运动的位移为x0-x=0.04m=4cm,根据位移时间关系可得
x0-x=![]() at2
at2
解得物块A、B由静止开始运动到分离所用的时间为
t=0.2s
故C错误、D正确。

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目