��Ŀ����
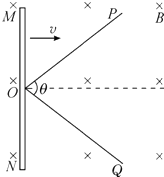
����Ŀ����ͼ��MN��PQ�ǵ��費�Ƶ�ƽ�н������죬����ΪL�������������ֹ⻬��ƽֱ���ֲִڣ��Ҷ˽�һ����ֵΪR�Ķ�ֵ���裮ƽֱ���ֵ�����������п���Ϊd��������ֱ���ϡ��Ÿ�Ӧǿ�ȴ�СΪB����ǿ�ų�������Ϊm������ҲΪR�Ľ������Ӹ�Ϊh����ֹ�ͷţ�����ų��ұ߽紦ǡ��ֹͣ����֪��������ƽֱ���ֵ����Ķ�Ħ������Ϊu���������뵼���Ӵ����ã�������������ų�����Ĺ����У� ��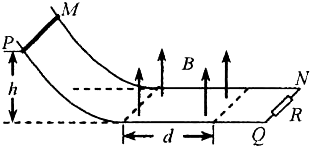
A.������������������Ϊ ![]()
B.ͨ���������ĵ����Ϊ ![]()
C.�˷������������Ĺ�Ϊmgh
D.�����������Ľ�����Ϊ ![]() mg��h����d��
mg��h����d��
���𰸡�D
���������⣺A���������»������У���е���غ㣬�ɻ�е���غ㶨�ɵã�mgh= ![]() mv2 �� ����������ˮƽ��ʱ���ٶ�v=
mv2 �� ����������ˮƽ��ʱ���ٶ�v= ![]() ������������ˮƽ����������˶����յ���ˮƽ��ʱ���ٶ��������Ӧ�綯��E=BLv������Ӧ����I=
������������ˮƽ����������˶����յ���ˮƽ��ʱ���ٶ��������Ӧ�綯��E=BLv������Ӧ����I= ![]() =
= ![]() ����A����
����A����
B����Ӧ�����q= ![]() ��t=
��t= ![]() ��t=
��t= ![]() ��t=
��t= ![]() =
= ![]() =
= ![]() ����B����
����B����
C���������������˶������У��ɶ��ܶ����ã�mgh��WB����mgd=0��0���˷�������������WB=mgh����mgd����C����
D���˷�����������ת��Ϊ�����ȣ������뵼���������ȣ�ͨ�����ǵĵ�����ȣ�������������Ľ�����
QR= ![]() Q=
Q= ![]() WB=
WB= ![]() mg��h����d������D��ȷ��
mg��h����d������D��ȷ��
��ѡ��D��
�����㾫����������Ĺؼ���������ܶ������ۺ�Ӧ�õ����֪ʶ������Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ��Լ��Ի�е���غ㼰�����������⣬�˽���ֻ���������͵��ɵ����������������£����嶯�ܺ��������ܣ����������ܣ������ת��������е�ܵ��������ֲ��䣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�