题目内容
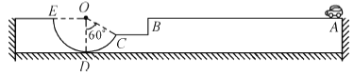
【题目】如图所示,水平轨道AB的距离L=8m,质量m=2kg、可视为质点的玩具车从A点以额定功率P=10W启动,车在AB段运动时的阻力恒为f=2N。当车由轨道边缘B点飞出后,恰能沿竖直光滑圆弧轨道CDE(D点为圆弧轨道的最低点)上C点的切线方向飞入圆弧轨道,且此时的速度大小为vC=6m/s,∠COD=60°,并从轨道边缘E点竖直向上飞出后上升的最大高度h=0. 8m。不计空气阻力,g取10m/s2,则
A.玩具车运动到B点时的速度大小为![]() m/s
m/s
B.玩具车发动机在水平轨道上工作的时间为0. 9s
C.圆弧轨道的半径为2m
D.玩具车对圆弧轨道的最大压力大小为56N
【答案】C
【解析】
A.玩具车运动到B点时的速度
![]()
代入数据解得
![]()
选项A错误;
B.从A到B的运动过程中有牵引力和阻力做功,根据动能定理有
![]()
代入数据解得
t=2. 5s
选项B错误;
CD.从C点运动到最大高度过程中,只有重力做功,所以机械能守恒,有
![]()
圆弧轨道的半径
R=2m
玩具车到达D点时对轨道的压力最大,玩具车在D点速度为vD,从C到D过程中机械能守恒有
![]()
![]()
代入数据得玩具车对轨道的最大压力
![]() N
N
选项C正确,D错误.
故选C。

 阅读快车系列答案
阅读快车系列答案【题目】某同学利用如图所示的向心力演示器定量探究匀速圆周运动所需向心力F跟小球质量m、转速n和运动半径r之间的关系。
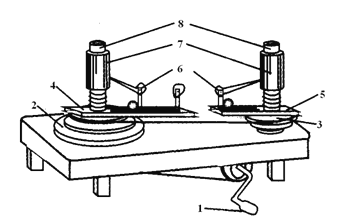
(1)为了单独探究向心力跟小球质量的关系,必须用________法;
(2)转动手柄可以使长槽和短槽分别随变速塔轮匀速转动,槽内的球随之做匀速圆周运动。这时我们可以看到弹簧测力筒上露出标尺,通过标尺上红白相间等分格数,即可求得两个球所受的________;
(3)该同学通过实验得到如下表的数据:
次数 | 球的质量m/g | 转动半径r/cm | 转速/每秒几圈 | 向心力大小F/红格数 |
1 | 14.0 | 15.00 | 1 | 2 |
2 | 28.0 | 15.00 | 1 | 4 |
3 | 14.0 | 15.00 | 2 | 8 |
4 | 14.0 | 30.00 | 1 | 4 |
根据以上数据,可归纳概括出向心力F跟小球质量m、转速n和运动半径r之间的关系是: ___________________(文字表述);
(4)实验中遇到的问题有:_________(写出一点即可)。