题目内容
4.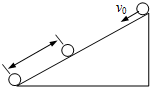 如图所示,小球在较长的斜面顶端,由静止开始以加速度a=2m/s2向下滑,在到达底端的前1s内,所滑过的距离为$\frac{7L}{16}$,其中L(未知)为斜面长,则
如图所示,小球在较长的斜面顶端,由静止开始以加速度a=2m/s2向下滑,在到达底端的前1s内,所滑过的距离为$\frac{7L}{16}$,其中L(未知)为斜面长,则(1)小球在斜面上滑行的时间为多少?
(2)斜面的长度L是多少?
分析 设总时间为t,结合位移时间公式,通过滑行的距离关系求出运动的时间.根据位移时间公式求出斜面的长度.
解答 解:(1)设小球在斜面上滑行的时间为t,则有:$\frac{1}{2}a{t}^{2}=L$,$\frac{1}{2}a(t-1)^{2}=\frac{9L}{16}$,
解得t=4s.
(2)斜面的长度L=$\frac{1}{2}a{t}^{2}=\frac{1}{2}×2×16m=16m$.
答:(1)小球在斜面上滑行的时间为4s;
(2)斜面的长度L为16m.
点评 解决本题的关键掌握匀变速直线运动的位移时间公式,通过位移关系求出运动的时间是解决本题的突破口.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
16.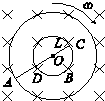 如图所示,一金属棒AC在匀强磁场中绕平行于磁感应强度方向的轴(过O点)匀速转动,OA=2OC=2L,磁感应强度大小为B、方向垂直纸面向里,金属棒转动的角速度为ω、电阻为r,内、外两金属圆环分别与C、A、D良好接触并从A、D各引出一接线柱与外电阻R相接(没画出),两金属环圆心皆为O且电阻均不计,则( )
如图所示,一金属棒AC在匀强磁场中绕平行于磁感应强度方向的轴(过O点)匀速转动,OA=2OC=2L,磁感应强度大小为B、方向垂直纸面向里,金属棒转动的角速度为ω、电阻为r,内、外两金属圆环分别与C、A、D良好接触并从A、D各引出一接线柱与外电阻R相接(没画出),两金属环圆心皆为O且电阻均不计,则( )
 如图所示,一金属棒AC在匀强磁场中绕平行于磁感应强度方向的轴(过O点)匀速转动,OA=2OC=2L,磁感应强度大小为B、方向垂直纸面向里,金属棒转动的角速度为ω、电阻为r,内、外两金属圆环分别与C、A、D良好接触并从A、D各引出一接线柱与外电阻R相接(没画出),两金属环圆心皆为O且电阻均不计,则( )
如图所示,一金属棒AC在匀强磁场中绕平行于磁感应强度方向的轴(过O点)匀速转动,OA=2OC=2L,磁感应强度大小为B、方向垂直纸面向里,金属棒转动的角速度为ω、电阻为r,内、外两金属圆环分别与C、A、D良好接触并从A、D各引出一接线柱与外电阻R相接(没画出),两金属环圆心皆为O且电阻均不计,则( )| A. | 金属棒中有从A到D的感应电流 | B. | 外电阻R中的电流为I=$\frac{9Bω{L}^{2}}{2(3R+r)}$ | ||
| C. | 当r=2R时,外电阻消耗功率最大 | D. | 金属棒AO间电压为$\frac{9BωR{L}^{2}}{2(3R+r)}$ |
19.现有电灯L1(3V、3W)和电灯L2(3V、6W)两只及一个可变电阻R(0→10Ω,5A),接在电压恒为6V的电路中,要求两只灯都正常发光,并且电路消耗功率最小,则应该用图中那个电路( )
| A. | 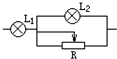 | B. | 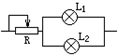 | C. |  | D. |  |
13.一质点做匀加速直线运动时,速度变化△v时发生位移x1,紧接着速度变化同样的△v时发生位移x2,则该质点的加速度为( )
| A. | (△v)2($\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$) | B. | 2$\frac{(△v)^{2}}{{x}_{1}-{x}_{2}}$ | C. | (△v)2($\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$) | D. | $\frac{(△v)^{2}}{{x}_{1}-{x}_{2}}$ |
14.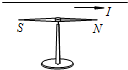 如图所示,把一条导线平行地放在磁针的上方附近,当电流通过导线时,磁针会发生偏转.首先观察到这个实验现象的物理学家是( )
如图所示,把一条导线平行地放在磁针的上方附近,当电流通过导线时,磁针会发生偏转.首先观察到这个实验现象的物理学家是( )
 如图所示,把一条导线平行地放在磁针的上方附近,当电流通过导线时,磁针会发生偏转.首先观察到这个实验现象的物理学家是( )
如图所示,把一条导线平行地放在磁针的上方附近,当电流通过导线时,磁针会发生偏转.首先观察到这个实验现象的物理学家是( )| A. | 奥斯特 | B. | 爱因斯坦 | C. | 法拉第 | D. | 欧姆 |
 .
.
 :量程3V,内阻3kΩ
:量程3V,内阻3kΩ :量程0~3A,内阻未知
:量程0~3A,内阻未知 为研究无线传输电能,某科研小组在实验室试制了无线电能传输装置,在短距离内点亮了灯泡,如图实验测得,接在乙线圈上的用电器获得的电能为输入甲线圈电能的35%.
为研究无线传输电能,某科研小组在实验室试制了无线电能传输装置,在短距离内点亮了灯泡,如图实验测得,接在乙线圈上的用电器获得的电能为输入甲线圈电能的35%.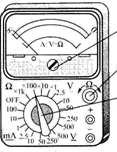 用多用电表测量电阻,将K旋转到电阻挡“×100”的位置,将两表笔分别与侍测电阻相接,发现指针偏转角度过小.为了得到比较准确的测量结果,请从下列选项中挑出合理的步骤,并按ADC的顺序避行操作,再完成读数测量.
用多用电表测量电阻,将K旋转到电阻挡“×100”的位置,将两表笔分别与侍测电阻相接,发现指针偏转角度过小.为了得到比较准确的测量结果,请从下列选项中挑出合理的步骤,并按ADC的顺序避行操作,再完成读数测量.