题目内容
2．
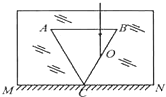如图所示，在屏幕MN的上方有空间足够大且折射率n=$\sqrt{3}$的玻璃介质，玻璃中有一正三角形空气泡，其边长l=40cm．顶点与屏幕接触于C点，底边AB与屏幕平行．一束光垂直于AB边射向BC边的中点O，结果在屏幕MN上出现两个光斑．则这两个光斑之间的距离为（ ）| A． | 10cm | B． | 20cm | C． | 30cm | D． | 40cm |
分析 光束垂直于AB边射向BC边的中点O时，由于光的反射和折射，在屏幕MN上出现两个光斑，由折射定律和折射定律作出光路图．由几何知识求出a光的入射角，由折射定律求出折射角，根据反射定律求出反射角．由几何知识求解两个光斑之间的距离．
解答 
解：画出光路图如图所示，在界面BC上，光的入射角i=60°．
由光的折射定律有：n=$\frac{sini}{sinr}$，代入数据，求得折射角r=30°
由光的反射定律得，反射角i′=60°．
由几何关系易得：△ODC是边长为0.5l的正三角形，△COE为等腰三角形，CE=OC=0.5l．故两光斑之间的距离L=DC+CE=l=40cm，故D正确．
故选：D．
点评 本题是几何光学问题，是折射定律、反射定律与几何知识的综合应用．要充分运用几何知识，求解两个光斑之间的距离．
练习册系列答案
轻松暑假总复习系列答案
相关题目
12．甲物体的重量比乙物体大3倍，甲从H高处自由落下，乙从3H高处与甲物体同时自由落下，忽略空气阻力，在它们落地之前，下列说法中正确的是（ ）
| A． | 两物体下落过程中，在同一时刻甲的速度比乙的速度大 | |
| B． | 各自下落1 m时，它们的速度相同 | |
| C． | 下落过程中甲的加速度比乙的加速度大 | |
| D． | 甲乙经过同一高度处，它们的速度相同 |
13．假如汽车在水平路面上加速直线运动时发动机的功率恒定不变，受的阻力也保持不变，则（ ）
| A． | 牵引力大小将恒定不变 | B． | 牵引力将均匀地增大 | ||
| C． | 牵引力将均匀地将小 | D． | 以上论断都不对 |
17．
在如图所示的电路中，开关S原来时闭合的，现将S断开，则灯泡L亮度变化和电容器C带电量变化情况是（ ）
在如图所示的电路中，开关S原来时闭合的，现将S断开，则灯泡L亮度变化和电容器C带电量变化情况是（ ）| A． | 灯泡L变亮、电容器C带电量增加 | B． | 灯泡L变亮、电容器C带电量减少 | ||
| C． | 灯泡L变暗、电容器C带电量增加 | D． | 灯泡L变暗、电容器C带电量减少 |
7．
如图是一种理想自耦变压器的示意图．线圈绕在一个圆环形的铁芯上，P是可移动的滑动触头．AB间接交流电压U，输出端接通了两个相同的灯泡L1和L2，Q为滑动变阻器的滑动触头．当开关S闭合，P处于如图所示的位置时，两灯均能发光．下列说法正确的是（ ）
如图是一种理想自耦变压器的示意图．线圈绕在一个圆环形的铁芯上，P是可移动的滑动触头．AB间接交流电压U，输出端接通了两个相同的灯泡L1和L2，Q为滑动变阻器的滑动触头．当开关S闭合，P处于如图所示的位置时，两灯均能发光．下列说法正确的是（ ）| A． | P不动，将Q向右移动，变压器的输入功率变大 | |
| B． | P不动，将Q向左移动，两灯均变暗 | |
| C． | P、Q都不动，断开开关S，L1将变暗 | |
| D． | Q不动，将P沿逆时针方向移动，变压器输入功率变大 |
14．下列各组物理量均为矢量的是（ ）
| A． | 位移、时间、速度 | B． | 速度、加速度、路程 | ||
| C． | 力、速度、位移 | D． | 力、速度变化量、重力加速度、质量 |
11．在圆轨道上运动的质量为m的人造地球卫星，它到地面的距离等于地球半径R，地面上的重力加速度为g，则（ ）
| A． | 卫星运动的速度为$\sqrt{2gR}$ | B． | 卫星运动的周期为4π$\sqrt{\frac{2R}{g}}$ | ||
| C． | 卫星运动的加速度为$\frac{g}{4}$ | D． | 卫星的动能为$\frac{mgR}{2}$ |
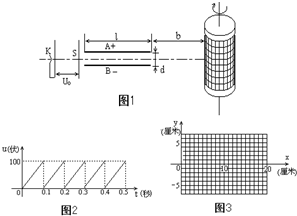如图1所示，真空室中电极K连续不断的发出电子，发出的电子（初速不计）经过U0=1000V的加速电场后，由小孔S沿两水平金属板A、B间的中心线射入．A、B板长l=0.20m，相距d=0.020m，加在A、B两板间的电压u随时间t变化的u-t图线如图2所示．设A、B间的电场可看做是均匀的，且两板外无电场．在分别每个电子通过电场区域的极短时间内，电场可视作恒定的匀强电场．两板右侧放一记录圆筒，筒的左侧边缘与极板右端距离b=0.15m，筒绕其竖直轴匀速转动，周期T=0.20s，筒的周长s=0.20m，筒能接收到通过A、B板的全部电子（不计电子间相互作用及电子重力）．