题目内容
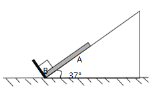
【题目】如图所示，在一倾角为37°的足够长的光滑斜面底端固定有挡板P，一个长木板A和物块B静止在斜面底端，mA=1kg，mB=3kg，初始时刻，物块B在长木板A的最下端，现在给物块B沿斜面向上的初速度，物块 B 可看成质点，g=10m/s2。则：
（1）当B获得一个速度后，若要木板 A 也能沿斜面向上运动，则 A、B之间的动摩擦因数需满足什么条件？
（2）若B的初速度为16m/s，动摩擦因数为0.5，要使物块B不从木板上端滑下来，木板的长度至少为多少？
（3）在满足（2）的条件下，木板沿斜面上升的最大距离为多少？
【答案】（1）
（2）
（3）
【解析】
考查运动学公式的应用，牛顿第二定律。
（1）若要木板A也能沿斜面向上运动，则AB间的摩擦力应满足：
解得；
（2）要使B不从长木板滑下，则长木板长度至少要满足两物体公共速时，B刚好滑到长木板上端，对A
解得
对B
解得
联立各式解得：
，
，
，
解得木板的长度至少为
（3）达到共速后，AB两物体保持相对静止，无摩擦力，一起向上做匀减速运动：
解得
，方向沿斜面向下，设共速后还能上升的位移为x，则：
解得
所以A能上升的最大高度为：
练习册系列答案
智能训练练测考系列答案
相关题目
