题目内容
【题目】如图所示,光滑的水平面AB与半径R=0.4m的光滑竖直半圆轨道BCD在B点相切,D点为半圆轨道最高点,A点的右侧连接一粗糙的水平面。用细线连接甲、乙两物体,中问夹一轻质压缩弹簧,弹簧与甲、乙两物体不拴接,甲的质量朋 ![]() =4kg,乙的质量
=4kg,乙的质量 ![]() =5kg,甲、乙均静止。若固定乙,烧断细线,甲离开弹簧后经过B点进入半圆轨道,过D点时对轨道的压力恰好为零。取g=10m/s2 , 甲、乙两物体均可看作质点,求:
=5kg,甲、乙均静止。若固定乙,烧断细线,甲离开弹簧后经过B点进入半圆轨道,过D点时对轨道的压力恰好为零。取g=10m/s2 , 甲、乙两物体均可看作质点,求:
(1)甲离开弹簧后经过B点时的速度的大小v2;
(2)在弹簧压缩量相同的情况下,若固定甲,烧断细线,乙物体离开弹簧后从A点进入动摩擦因数 ![]() =0.4的粗糙水平面,则乙物体在粗糙水平面运动的位移S。
=0.4的粗糙水平面,则乙物体在粗糙水平面运动的位移S。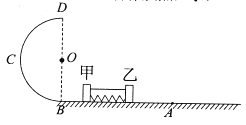
【答案】
(1)
甲在最高点D,由牛顿第二定律得: ![]() ,设甲离开弹簧运动至D点的过程中机械能守恒得:
,设甲离开弹簧运动至D点的过程中机械能守恒得: ![]() m1vB2=m1g2R+
m1vB2=m1g2R+ ![]() m1vD2.
m1vD2.
代入数据联立解得:vB=2 ![]() m/s.
m/s.
(2)
甲固定,烧断细线后乙的速度大小为v2,由能量守恒得:
Ep= ![]() m1vB2=
m1vB2= ![]() m2v22,
m2v22,
得:v2=4m/s.
乙在粗糙水平面做匀减速运动:μm2g=m2a,
解得:a=4m/s2,
则有: ![]()
【解析】(1)甲在最高点D , 由牛顿第二定律得: ![]() ,设甲离开弹簧运动至D点的过程中机械能守恒得:
,设甲离开弹簧运动至D点的过程中机械能守恒得: ![]() m1vB2=m1g2R+
m1vB2=m1g2R+ ![]() m1vD2 .
m1vD2 .
代入数据联立解得:vB=2 ![]() m/s.(2)甲固定,烧断细线后乙的速度大小为v2 , 由能量守恒得:
m/s.(2)甲固定,烧断细线后乙的速度大小为v2 , 由能量守恒得:
Ep= ![]() m1vB2=
m1vB2= ![]() m2v22 ,
m2v22 ,
得:v2=4m/s.
乙在粗糙水平面做匀减速运动:μm2g=m2a ,
解得:a=4m/s2 ,
则有: ![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目