题目内容
用两轻绳的末端各系质量分别为mA、、mB的带同种电荷的小球，两绳另一端同系于O点，如图所示，绳长分别为LA、、LB，且mB=2mA，LA=2LB，平衡后绳与竖直方向夹角分别为
、β．关于两夹角的大小关系，正确的判断是（ ）
、β．关于两夹角的大小关系，正确的判断是（ ）| A．α=β | B．α<β | C．α>β | D．无法确定 |
A
这是一个平衡问题。
将两个小球以及两根绳子作为系统，系统受到的外力（不是内力）有：A的重力、B的重力、O点对两绳的拉力，合力为0，而且合力矩也为0。
用合力矩为0来做，O点是支点（轴），则有
mA*g*LA*sinα＝mB*g*LB*sinβ
得 sinα / sinβ＝mB*LB / (mA*LA)＝2*mA*LB / (mA*2LB)＝1
即 sinα ＝ sinβ
因 α、β都是锐角，所以得 α＝β
将两个小球以及两根绳子作为系统，系统受到的外力（不是内力）有：A的重力、B的重力、O点对两绳的拉力，合力为0，而且合力矩也为0。
用合力矩为0来做，O点是支点（轴），则有
mA*g*LA*sinα＝mB*g*LB*sinβ
得 sinα / sinβ＝mB*LB / (mA*LA)＝2*mA*LB / (mA*2LB)＝1
即 sinα ＝ sinβ
因 α、β都是锐角，所以得 α＝β
练习册系列答案
相关题目
、
(
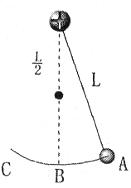
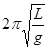
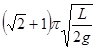
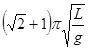
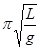
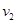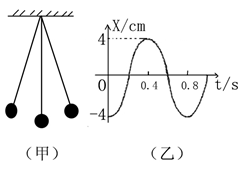
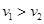)在竖直平面内做小角度摆动，它们的频率与振幅分别为
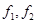和
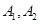，则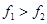
，
，
，
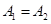
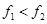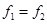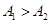
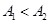
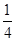时，周期为 ；若只将摆球质量减为原来的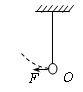
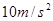，试求这个摆的摆长是多少？