题目内容
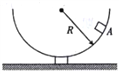
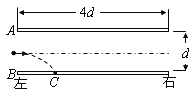
【题目】如图所示，长为9l水平传送带以恒定的速度
作顺时针转动，紧邻传送带的右端放置一长为6.5l滑板，滑板静止在光滑水平地面上，滑板的上表面与传送带处在同一水平面。在距滑板右端一段距离处固定一挡板C。一质量为m的物块被轻放在传送带的最左端（A点），物块在传送带的作用下到达B点后滑上滑板，滑板在物块的怍用下运动到C处撞上档板并被牢固粘连。物块可视为质点，滑板的质量M=2m，物块与传送带、物块与滑板间的动摩擦因数均为
，重力加速度取g。求：
（1）求物块在传送带的作用下运动到B点时的速度大小v；
（2）若物块和滑板共速时，滑板恰与挡板C相撞，求开始时滑板右端到C的距离L；
（3）若滑板右端到挡板C的距离为L（己知），且l≤L≤5l，试求解：
a. 若物块与滑板共速后，滑板撞上挡板C，则物块从滑上滑板到物块撞上档板C的过程中，物块克服摩擦力做的功
；
b. 若物块与滑板共速前，滑板撞上挡板C，则物块从滑上滑板到物块撞上档板C的过程中，物块克服摩擦力做的功
；并求出物块到C时速度的最大值。
【答案】（1）
（2）2l （3）a. 
b. 
【解析】(1)设物块到达B点的速度为vB，对物块从A到B由动能定理得： 
解得
< 
，所以物块一直加速，运动到B点时的速度大小
（2）假设物块与滑板达到共同速度v时，物块还没有离开滑板，对物块与滑板，由动量守恒，有
③
设物块在滑板上运动的距离为s1，由能量守恒得
④
联立解得s1=6R<6.5R ⑤
即达到共同速度v时，物块不会脱离滑板滑下。
设此过程滑板向右运动的距离为s2，对滑板由动能定理得
⑥
解得s2=2l
（3）讨论：①当l<L<2l时，滑块在滑板上一直减速到右端，设此时的速度为vC，对物块由动能定理得
⑦
解得
所以克服摩擦力所做的功
= 
②当2l≤L≤5l时，滑块与滑板最终一起运动至滑板与C相碰，碰后滑块在滑板上继续做减速运动到右端，设此时的速度为vC1，对物块由动能定得：
⑨
解得
〉0
所以克服摩擦力所做的功
