题目内容
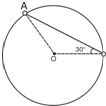如图所示，光滑圆环固定在竖直平面上，环上穿过带孔小球A、B，两球用轻绳系着，平衡时细绳与水平方向的夹角为30°，此时球B恰与环心O在同一水平面上，求A球与B球的质量之比．分析：先以B球研究对象，分析受力情况，根据平衡条件求出细绳对B球的拉力．再对A球研究，分析受力情况，运用正交分解法求解A球的质量．
解答：解：对A、B两球研究，分析受力情况如图所示，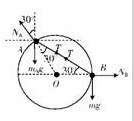
对B球，由平衡条件得：
Tsin30°=mBg，解得T=2mBg ①；
对A球，由平衡条件得：
在水平方向：Tcos30°=NAsin30° ②，
在竖直方向：NAcos30°=mAg+Tsin30° ③，
由①②③解得：mA=2mB，则mA：mB=2：1．
答：A球与B球的质量之比为mA：mB=2：1
对B球，由平衡条件得：
Tsin30°=mBg，解得T=2mBg ①；
对A球，由平衡条件得：
在水平方向：Tcos30°=NAsin30° ②，
在竖直方向：NAcos30°=mAg+Tsin30° ③，
由①②③解得：mA=2mB，则mA：mB=2：1．
答：A球与B球的质量之比为mA：mB=2：1
点评：本题采用隔离法研究物体的平衡问题，正确分析受力，作出力图是关键．
练习册系列答案
相关题目
如图所示，两个金属轮A1、A2，可绕通过各自中心并与轮面垂直的固定的光滑金属细轴O1和O2转动，O1和O2相互平行，水平放置．每个金属轮由四根金属辐条和金属环组成，A1轮的辐条长为a1、电阻为R1，A2轮的辐条长也为a1、电阻为R2，连接辐条的金属环的宽度与电阻都可以忽略．半径为a0的绝缘圆盘D与A1同轴且固连在一起，一轻细绳的一端固定在D边缘上的某点，绳在D上绕足够匝数后，悬挂一质量为m的重物P．当P下落时，通过细绳带动D和A1绕轴转动．转动过程中A1、A2保持接触，无相对滑动；两轮与各自轴之间保持良好接触，无相对滑动；两轮与各自细轴之间保持良好的电接触；两细轴通过导线与一阻值为R的电阻相连．除R和A1、A2两轮中辐条的电阻外，所有金属电阻都不计．整个装置处在磁感应强度为B的匀强磁场中，磁场方向与转轴平行，现将P由静止起释放，
