题目内容
16.某人在一星球上以速率v竖直上抛一物体,经时间t物体以速率v落回手中,已知该星球的半径为R,求这星球上的第一宇宙速度$\sqrt{\frac{2vR}{t}}$.分析 根据竖直上抛运动的对称性,结合速度时间公式求出星球表面的重力加速度,结合重力提供向心力求出星球上的第一宇宙速度.
解答 解:根据竖直上抛运动的对称性知,星球表面的重力加速度g=$\frac{v}{\frac{t}{2}}=\frac{2v}{t}$,
根据mg=$m\frac{{v}^{2}}{R}$得,星球上的第一宇宙速度v=$\sqrt{gR}=\sqrt{\frac{2vR}{t}}$.
故答案为:$\sqrt{\frac{2vR}{t}}$.
点评 本题考查了竖直上抛运动与万有引力定律的综合,知道第一宇宙速度等于贴近星球表面做匀速圆周运动的速度,抓住重力提供向心力进行求解.

练习册系列答案
相关题目
7.2008年9月25日至28日我国成功实施了“神舟”七号载入航天飞行并实现了航天员首次出舱.飞船先沿椭圆轨道飞行,后在远地点343千米处点火加速,由椭圆轨道变成高度为343千米的圆轨道,在此圆轨道上飞船运行周期约为90分钟.下列判断正确的是( )
| A. | 飞船变轨前后的机械能相等 | |
| B. | 飞船在圆轨道上时航天员出舱前后都处于失重状态 | |
| C. | 飞船在此圆轨道上运动的角速度大于同步卫星运动的角速度 | |
| D. | 飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度 |
11. 发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,下列说法中正确的是( )
发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,下列说法中正确的是( )
 发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,下列说法中正确的是( )
发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,下列说法中正确的是( )| A. | 卫星在轨道3上的速率大于在轨道1上的速率 | |
| B. | 卫星在轨道3上的角速度小于在轨道1上的角速度 | |
| C. | 卫星在轨道1上经过Q点时的加速度大于它在轨道2上经过Q点时的加速度 | |
| D. | 卫星在轨道2上经过P点时的加速度小于它在轨道3上经过P点时的加速度 |
1.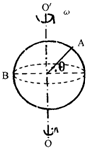 花式篮球是年青人酷爱的一项运动,图示为某同学在单指转篮球,篮球绕中心线OO′匀速转动,A、B为篮球表面不同位置的两点,则( )
花式篮球是年青人酷爱的一项运动,图示为某同学在单指转篮球,篮球绕中心线OO′匀速转动,A、B为篮球表面不同位置的两点,则( )
 花式篮球是年青人酷爱的一项运动,图示为某同学在单指转篮球,篮球绕中心线OO′匀速转动,A、B为篮球表面不同位置的两点,则( )
花式篮球是年青人酷爱的一项运动,图示为某同学在单指转篮球,篮球绕中心线OO′匀速转动,A、B为篮球表面不同位置的两点,则( )| A. | B点的角速度大于A点角速度 | B. | A、B两点线速度大小相等 | ||
| C. | A、B两点的周期相等 | D. | A、B两点向心加速度大小相等 |
8.某质点作简谐振动,从质点经过某一位置时开始计时( )
| A. | 当质点再次经过此位置时,所经历的时间是一个周期 | |
| B. | 当质点的速度再次与零时刻的速度相同时,所经历的时间是一个周期 | |
| C. | 当质点的加速度与零时刻的加速度再次相同时,所经历的时间是一个周期 | |
| D. | 以上三种说法均不正确 |
5.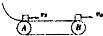 如图所示,水平传送带A、B两端相距x=3.5m,物体与传送带间的动摩擦因数μ=0.1,物体滑上传送带A端的瞬时速度vA=4m/s,到达B端的瞬时速度设为vB,下列说法中正确的是( )
如图所示,水平传送带A、B两端相距x=3.5m,物体与传送带间的动摩擦因数μ=0.1,物体滑上传送带A端的瞬时速度vA=4m/s,到达B端的瞬时速度设为vB,下列说法中正确的是( )
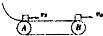 如图所示,水平传送带A、B两端相距x=3.5m,物体与传送带间的动摩擦因数μ=0.1,物体滑上传送带A端的瞬时速度vA=4m/s,到达B端的瞬时速度设为vB,下列说法中正确的是( )
如图所示,水平传送带A、B两端相距x=3.5m,物体与传送带间的动摩擦因数μ=0.1,物体滑上传送带A端的瞬时速度vA=4m/s,到达B端的瞬时速度设为vB,下列说法中正确的是( )| A. | 若传送带逆时针匀速转动,vB一定等于3m/s | |
| B. | 若传送带逆时针匀速转动越快,vB越小 | |
| C. | 若传送带顺时针匀速转动,vB有可能等于3m/s | |
| D. | 若传送带顺时针匀速转动,物体刚开始滑上传送带A端时一定做匀加速运动 |
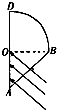 一块玻璃砖折射率为n=2,由四分之一圆柱和横截面为等腰直角三角形的棱柱组合而成,此玻璃砖的横截面如图所示,圆半径为R,一束平行光垂直AB照射到OA上,求圆弧BD上有光射出部分的弧长.
一块玻璃砖折射率为n=2,由四分之一圆柱和横截面为等腰直角三角形的棱柱组合而成,此玻璃砖的横截面如图所示,圆半径为R,一束平行光垂直AB照射到OA上,求圆弧BD上有光射出部分的弧长.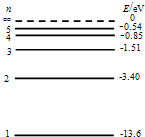 某个光子是氢原子核外电子从n=4跃迁到n=1时所发出的,已知普朗克常量h=6.63×10-34J•s,求:
某个光子是氢原子核外电子从n=4跃迁到n=1时所发出的,已知普朗克常量h=6.63×10-34J•s,求: