题目内容
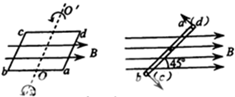如图a所示，一矩形线圈abcd放置在匀强磁场中，并绕过ab、cd中点的轴OO′以角速度ω逆时针匀速转动．若以线圈平面与磁场夹角θ=45°时（如图b）为计时起点，并规定当电流自a流向b时电流方向为正．则下列四幅图中正确的是（ ）
分析：从a图可看出线圈从垂直于中性面开始旋转，所以是余弦函数，根据楞次定律可以判断出电流方向，写出电流的瞬时表达式即可求解．
解答：解：从a图可看出线圈从垂直于中性面开始旋转，由楞次定律可判断，初始时刻电流方向为b到a，故瞬时电流的表达式为i=-imcos(ωt+
π)，故D正确．
故选D
| 1 |
| 4 |
故选D
点评：本题考查正弦交流电的产生过程、楞次定律等知识和规律，难度适中．
练习册系列答案
名校课堂系列答案
相关题目
（2008?宣武区三模）如图所示，一矩形线框以竖直向上的初速度进入只有一 条水平边界的匀强磁场，磁场方向垂直纸面向里，进入磁场后上升一段高度又落下离开磁场，运动中线框只受重力和磁场力，线框在向上、向下经过图中1、2位置时的速率按时间顺序依次为v1、v2、v3和v4，则可以确定（ ）
（2013?南京模拟）如图所示，一矩形线框置于磁感应强度为B的匀强磁场中，线框平面与磁场方向平行，若线框的面积为S，则通过线框的磁通量为（ ）
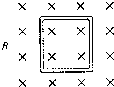如图所示，一矩形线框置于磁感应强度为B的匀强磁场中，线框平面与磁场方向垂直，若线框的面积为S，则通过线框的磁通量为（ ）| A、O | ||
B、
| ||
C、
| ||
| D、BS |
时刻线圈中感应电动势最大 
时刻导线ad的速度方向跟磁感线垂直
时刻线圈平面与中性面垂直 
、
两时刻线圈中感应电流方向相同
