题目内容
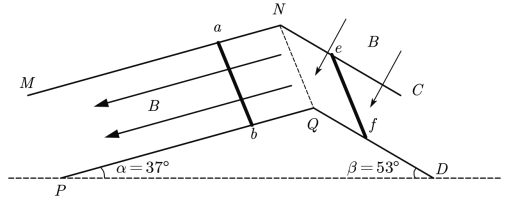
【题目】如图所示，足够长的金属导轨MNC和PQD平行且间距为L左右两侧导轨平面与水平面夹角分别为α=37°、β=53°，导轨左侧空间磁场平行导轨向下，右侧空间磁场垂直导轨平面向下，磁感应强度大小均为B。均匀金属棒ab和ef质量均为m，长度均为L，电阻均为R，运动过程中，两金属棒与导轨保持良好接触，始终垂直于导轨，金属棒ab与导轨间的动摩擦因数为μ=0.5，金属棒ef光滑。同时由静止释放两金属棒，并对金属棒ef施加外力F，使ef棒保持a=0.2g的加速度沿斜面向下匀加速运动。导轨电阻不计，重力加速度大小为g，sin37°=0.6，cos37°=0.8。求：
（1）金属棒ab运动过程中最大加速度的大小；
（2）金属棒ab达到最大速度所用的时间；
（3）金属棒ab运动过程中，外力F对ef棒的冲量。
【答案】（1）
；（2）
；（3）
，负号代表冲量沿斜面向上。
【解析】
（1）金属棒ab释放瞬间加速度最大，根据牛顿第二定律有
得
（2）金属棒ab释放之后，合外力为零时速度最大，则有
其中
得
（3）金属棒ab释放之后，根据牛顿第二定律，可得任意时刻的加速度
得：
，其图象如图所示
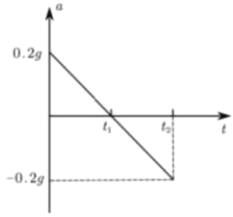
图像面积代表速度增量，由运动的对称性可知，从金属棒ab释放起，经过时间
速度减为零，此后保持静止，在此过程中，金属ef一直匀加速直线运动，则有
对金属棒ef，规定沿斜面向下为正方向，由动量定理可得
其中
得：，负号代表冲量沿斜面向上
说明：其它方法求解也可以，如写出外力
的表达式，用其平均值计算冲量大小
得
则可知释放瞬间，
时刻，
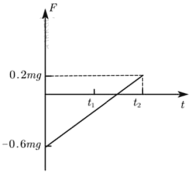
图象所围成的面积代表其冲量，则有
得：，负号代表冲量沿斜面向上
练习册系列答案
相关题目
