Question

【题目】如图所示，半径为R的半圆形管道ACB固定在竖直平面内，倾角为θ的斜面固定在水平面上，细线跨过小滑轮连接小球和物块，细线与斜面平行，物块质量为m，小球质量M＝3m，对物块施加沿斜面向下的力F使其静止在斜面底端，小球恰在A点．撤去力F后，小球由静止下滑．重力加速度为g，sin θ＝≈0.64，不计一切摩擦．求：

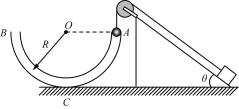
(1) 力F的大小；

(2) 小球运动到最低点C时，速度大小v以及管壁对它弹力的大小N；

(3) 在小球从A点运动到C点过程中，细线对物块做的功W.

Answer 1

【答案】(1) 2.36mg (2) 6mg (3) mgR.

【解析】

(1) 对小球：细线上的拉力T＝3mg

对物块：mgsin θ＋F＝T

解得F＝2.36mg.

(2) 小球在C点时速度与物块速度大小相等．

对小球和物块组成的系统，由机械能守恒定律

3mgR－mgπRsin θ＝ (3m＋m)v2

解得v＝

在C点：对小球，由牛顿第二定律N－3mg＝3m

解得N＝6mg .

(3) 在小球从A点运动到C点过程中，对物块，由动能定理

W－mgπRsin θ＝mv2－0

解得W＝mgR.